

 |
99 reken- en wiskunde puzzels |  |
 |
|
Bij sommige puzzels kan de freeware van deze website handig zijn. De puzzels zijn ook een prima uitgangspunt voor werkstukken. |
Een .pdf bestand met antwoorden en uitwerkingen wordt op aanvraag verzonden. |
| omschrijving | soort | |
|---|---|---|
| 1 | gemiddelde | rekenen |
| 2 | hoeveel beesten | rekenen |
| 3 | planeten | rekenen |
| 4 | welkomst pakketten | rekenen |
| 5 | puzzlestukjes | rekenen |
| 6 | lijnspiegeling | meetkunde |
| 7 | snijpunt | meetkunde |
| 8 | kosten besparen | rekenen/procenten |
| 9 | drinkwater | rekenen/algebra |
| 10 | touwtje | rekenen/tellen |
| 11 | broodjes | rekenen/tellen |
| 12 | regenmeter | algebra/meetkunde | 13 | balans 1 | algebra |
| 14 | balans 2 | algebra |
| 15 | haakjes | rekenen |
| 16 | Pietertje | rekenen |
| 17 | de erfenis | wiskunde/getaltheorie |
| 18 | Controle | wiskunde/getaltheorie |
| 19 | Archimedes | natuurkunde |
| 20 | Dichtheid | natuurkunde |
| 21 | IJsberg | natuurkunde |
| 22 | ...berekenen | natuurkunde |
| 23 | Potloden slijpen | wiskunde |
| 24 | De scheve boom | goniometrie |
| 25 | De schutters | ongelijkheden |
| 26 | Pendeldienst | wiskunde,rekenen |
| 27 | Draaicirkel | wiskunde,goniometrie |
| 28 | Wegennet | meetkunde |
| 29 | De brulboei | wiskunde |
| 30 | Robot | meetkunde |
| 31 | p berekenen | algebra |
| 32 | Een gek getal | rekenen |
| 33 | Lichtstraal | getallenleer |
| 34 | vierkant | getallenleer |
| 35 | Klassengrootte | rekenen |
| 36 | Stelling 1 | meetkunde |
| 37 | Stelling 2 | meetkunde |
| 38 | constructie 1 | meetkunde |
| 39 | constructie 2 | meetkunde |
| 40 | Bootje | algebra |
| 41 | Examen | algebra |
| 42 | LadderCurve | differentiaalrekening |
| 43 | Expeditie | differentiaal verg. |
| 44 | Telefoon | tellen |
| 45 | Olievat | goniometrie |
| 46 | Piramide | gonio-/stereometrie |
| 47 | Maanbasis | algebra |
| 48 | Treintjes | redeneren/rekenen |
| 49 | Deelbaar door 17? | algebra |
| 50 | De vriendelijke familie | redeneren |
| 51 | De schudrobot | redeneren |
| 52 | Duizenden | redeneren |
| 53 | Veelvoud | algebra |
| 54 | Tegels | redeneren |
| 55 | Veren | algebra |
| 56 | Rotatie | meetkunde |
| 57 | Verschuiving | meetkunde |
| 58 | Vereenvoudig | algebra |
| 59 | Marathon | algebra/redeneren |
| 60 | Trappen klimmen | redeneren |
| 61 | Hoeveel deelnemers? | rekenen/verhoudingen |
| 62 | Merkwaardige Producten | algebra |
| 63 | Ackermann functie | algebra |
| 64 | driehoek | meetkunde/verhoudingen |
| 65 | cirkel | algebra |
| 66 | de Galaxianen | algebra |
| 67 | hoek berekenen | meetkunde |
| 68 | het Wilde Westen | rekenen |
| 69 | Parket leggen | redeneren |
| 70 | geboortejaar | rekenen (programmeren) |
| 71 | Rekentruc | rekenen |
| 72 | Communicerende vaten | algebra |
| 73 | het Kettinkje | redeneren |
| 74 | de verdwenen streep | redeneren,rekenen |
| 75 | Rooster (2d) | algebra |
| 76 | Rooster (3d) | algebra |
| 77 | Draden tellen | redeneren |
| 78 | priemgetallen | redeneren/algebra |
| 79 | rugzak | algebra |
| 80 | bevolking | redeneren |
| 81 | bereken | breuken/algebra |
| 82 | geknikte functies | algebra/grafieken |
| 83 | gelijke oppervlakten | meetkunde |
| 84 | Wortel 2 | rekenen/redeneren |
| 85 | pompen | rekenen/redeneren |
| 86 | zagen | rekenen/algebra |
| 87 | verhoudingen | meetkunde voor gevorderden |
| 88 | de Prinses en de Draak | algebra |
| 89 | Evenwijdig | meetkunde |
| 90 | Vlot in Vijver | algebra |
| 91 | Rechthoek | algebra |
| 92 | parallellogram | meetkunde |
| 93 | de Torens van Hanoi | algebra, redeneren |
| 94 | bordspel(1) | redeneren |
| 95 | bordspel(2) | redeneren |
| 96 | Curve berekenen | differentiaalrekening |
| 97 | knuffelberen | redeneren |
| 98 | Loodlijn construeren | meetkunde |
| 99 | Letterpuzzel | redeneren |
1.gemiddelde
Een apparaat bestaat uit 3 onderdelen: motor, pomp en regelaar.
Van elk onderdeel is het volgende bekend:
| onderdeel | gemiddelde tijd tussen 2 storingen |
|---|---|
| motor | 8000 uur |
| pomp | 6000 uur |
| regelaar | 10000 uur |
Hoe groot is de gemiddelde tijd tussen twee storingen van het gehele apparaat?
2.hoeveel beesten?
Een boer heeft koeien en varkens in de verhouding 2:7
en varkens en kippen in de verhouding 3:19.
Er zijn totaal 320 beesten.
Hoeveel van elke soort?
3.planeten
In een ver verwijderd zonnenstelsel draaien 3 planeten rond met omlooptijden
van 189, 441 en 462 dagen.
Hoeveel dagen verlopen er tussen twee dezelfde standen?
4.welkomstpakketten
Een verpakkingsbedrijf moet zoveel mogelijk gelijke pakketten samenstellen
uit 3627 pakjes stroopwafels, 6045 blikjes vis en 9672 potjes jam.
Er mag niets overblijven.
Hoeveel pakketten worden dat en wat is de inhoud?
5.puzzlestukjes
Een legpuzzle bestaat uit 1247 stukjes.
Hoeveel van die stukjes hebben minstens 1 rechte rand?
6.lijnspiegeling

Spiegel het punt P in de lijn l en gebruik alleen een passer.
7.snijpunt
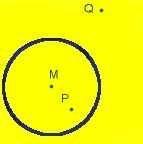 Gegeven is een cirkel met middelpunt M, een punt P binnen de cirkel
Gegeven is een cirkel met middelpunt M, een punt P binnen de cirkelen een punt Q erbuiten.
Construeer het snijpunt van de lijn PQ met de cirkel en
gebruik daarbij alleen een passer.
8.kosten besparen
a.
Een automobilist rijdt gewoonlijk 750km. op een volle tank benzine.
Door een rustiger rijstijl weet hij daar echter 824km. van te maken.
Hoeveel procent bespaart hij zodoende op brandstofkosten?
b.
Drie fabrikanten produceren tubes tandpasta met gelijke inhoud tegen
dezelfde prijs.
Ze besluiten tot een reclamestunt:
- A verhoogt de inhoud van een tube met 24% en houdt de prijs gelijk
- B verlaagt de prijs van een tube met 21% bij gelijke inhoud
- C verhoogt de inhoud met 11% en verlaagt tevens de prijs met 11%
Welke tandpasta is nu het goedkoopst in het gebruik?
9.drinkwater
De inwoners van een bergdorp betrekken hun drinkwater deels uit een
reservoir, dat gelijkmatig door een bron wordt bijgevuld.
Per bewoner wordt dagelijks gemiddeld een gelijke hoeveelheid water verbruikt.
Toen het dorp 800 inwoners telde, kon een vol reservoir 300 dagen in de behoefte
van het dorp voorzien.
Thans telt het dorp 1000 inwoners en het reservoir kan voor 200 dagen
water leveren.
Gedurende hoeveel dagen kan het reservoir in de drinkwaterbehoefte voorzien
als het dorp 1200 inwoners telt?
10.touwtje
Op hoeveel manieren kan een touwtje van 25cm. in drie stukken worden
verdeeld als:
- er alleen op hele cm. mag worden geknipt en
- de volgorde van de stukken er niet toe doet?
11.broodjes
Een bakker verkoopt broodjes in zakjes van 5 en 8 stuks.
Als je dus 4,6 of 17 broodjes koopt, dan moet hij een zakje openknippen
om het juiste aantal te krijgen.
Wat is de maximale bestelling waarbij nog een zakje moet worden opengeknipt?
12.regenmeter
Een regenmeter betaat uit een kegelvormig glazen vaasje, dat met de punt
omlaag in een houder is geplaatst.
Op het glas is een schaalverdeling aangebracht om de regenval (in mm.) weer te geven.
De regenmeter heeft een cirkelvormige opening met straal R, de diepte is H mm.
a. wat zou het voordeel zijn van de kegel- boven een rechthoekige vorm?
b. bedenk een formule, die aangeeft welk getal voor de neerslag N er op
de schaal moet staan bij hoogte h boven de punt.{N = f(h) }
c. wat is de invloed van R en van H op de nauwkeurigheid?{plat vs. hoog en smal}
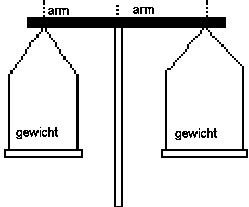 13. balans 1
13. balans 1Een balans is in evenwicht als links en rechts de
som van de koppels gelijk is.
Het koppel is het produkt van gewicht en de
armlengte.
Stel eens, dat het gewicht links 140 gram
bedraagt, het gewicht rechts 185 gram en dat
beide armen 25cm. lang zijn.
Op welke afstand van het middelpunt zou dan (links of rechts) een gewicht
van 66,6 gram moeten worden opgehangen om evenwicht te maken?
14.balans 2.
Zie vorig probleem voor uitleg balans.
Een balans heeft armen van ongelijke lengte.
Als een onbekend gewicht links hangt, moet rechts het gewicht 28 gram zijn
voor evenwicht.
Als het onbekende gewicht rechts hangt, moet links het gewicht 63 gram zijn
voor evenwicht.
Bereken het onbekende gewicht.
Bedenk een formule voor het onbekende gewicht X als voor evenwicht
de gewichten m1 en m2 nodig zijn.
15. Haakjes.
In de berekeningen hieronder zijn steeds 2 paar haakjes weggelaten.(..)..(..)
Plaats deze haakjes zo, dat de berekening klopt.
2009 = 9*8*7-6+5*4-3*2-1
2009 = 1+2+3^4-5+6*7*8+9
2010 = 1*2*3*4*5*6+7*8-9
16. Pietertje.
Pietertje wordt elke dag door zijn moeder van school gehaald. Precies als de
school uitgaat, komt moeder aanrijden.
Op een dag gaat de school 45 minuten eerder uit dan gewoonlijk. Pietertje
besluit zijn moeder tegemoet te lopen. Na enige tijd komt hij haar tegen,
Pietertje stapt in en ze rijden naar huis. Daar komen zij 16 minuten vroeger dan
gewoonlijk aan.
Hoe lang heeft Pietertje gelopen?
17. De Erfenis.
Een verzamelaar van schilderijen laat voor zijn kinderen het volgende
testament na:
| Amalia : | schenk 9 schilderijen naar keuze aan een museum en kies daarna zelf een zesde deel |
| Floris : | schenk van de resterende schilderijen er 6 aan een museum en kies daarna zelf een vierde deel |
| Roderick : | schenk 3 schilderijen aan een museum en kies daarna zelf een derde deel |
| Eloise : | kies de helft van de overgebleven schilderijen |
| Archibald : | de rest van de schilderijen is voor jou |
Uit hoeveel schilderijen moet deze erfenis minimaal bestaan?
18. Controle.
Jansen controleert elke 46 dagen het koelwater van zijn auto en elke
28 dagen de ruitenwisservloeistof.
Vandaag is het koelwater aan de beurt en over precies 12 dagen de
ruitenwisservloeistof.
Over hoeveel dagen vallen de controles op dezelfde dag?
19. De wet van Archimedes.
Een steen heeft onder water minder gewicht dan erboven. Dat komt door
de opwaartse kracht, die het water uitoefent.
Volgens de ontdekker van deze wet, Archimedes, is de opwaartse kracht
even groot als het gewicht van het water, dat de steen heeft weggedrukt.
Een rechthoekige steen heeft afmetingen 5 x 10 x 20 cm3 en weegt 2350 gram.
Hoeveel zal de steen onder water wegen?
20. Dichtheid.
Een van de eigenschappen van een stof is de dichtheid.
Daaronder wordt verstaan het gewicht van een volume-eenheid.
We nemen hiervoor het aantal grammen per ml. of kg. per liter, dat levert
hetzelfde getal op.
Voorbeeld: koper heeft een dichtheid van 8,92 (gram per ml.) en zink heeft
een dichtheid van 7,14.
Opmerking: een volume V van een stof met dichtheid D heeft een gewicht van
M = D x V.
In een laboratorium worden 100 gram koper en 150 gram zink samengesmolten.
Wat zal de dichtheid zijn van deze legering?
21. IJsberg.
IJs heeft een dichtheid van 0,98 en zeewater van 1,05.
Welk percentage van een ijsberg steekt boven water uit?
22. Dichtheid berekenen.
Een blokje van een onbekend metaal weegt 137,4 gram. Onder water is dat
echter 130,3 gram.
Welke dichtheid heeft dit metaal?
Bedenk een formule voor de dichtheid van een stof, als het gewicht
boven water M1 en onder water M2 bedraagt
23. Potloden Slijpen.
Een potlood bestaat uit een houten cilinder met in de kern een smalle
cilinder van grafiet.
Bij het slijpen van een potlood gaat veel materiaal verloren.
Stel een formule op voor het rendement y (= deel van het grafiet dat op
papier komt) als het potlood puntig wordt geslepen zodra de lijndikte het
x de deel (0,1..0,2..0,3...) van de diameter van het grafiet bedraagt.
Is de slijphoek van invloed op dit rendement?
24. De scheve boom.
Een boom staat 30 graden scheef, maar Pietertje kijkt vanuit een zodanige
positie dat de boom recht lijkt te staan.
Vervolgens loopt hij x graden over een cirkelboog rond de boom.
Vanuit deze nieuwe positie lijkt de boom y graden scheef te staan.
Opmerking: 30 graden scheef betekent een hoek van 60 graden met de grond.
Stel een formule op, die het verband geeft tussen x en y.
25. De Schutters.
Twee boogschutters, A en B, houden een wedstrijd. Ze schieten in hun eigen tempo
pijlen af op een doel. Elk houdt voor zichzelf het aantal missers en treffers
bij. Op een gegeven moment heeft A 23 keer raak geschoten terwijl B 14 keer heeft gemist.
Terwijl er nog pijlen over zijn wordt de strijd gestaakt omdat A toch heeft gewonnen.
Met hoeveel pijlen begon elke schutter?
Stel, dat elk begint met P pijlen en dat A heeft gewonnen als A Tatreffers
en Ma missers heeft (B: Tb en Mb)
Stel een ongelijkheid op die klopt als verder schieten geen zin heeft omdat A
toch heeft gewonnen.
26. Pendeldienst.
Een rederij onderhoudt met veerboten een pendeldienst tussen twee havensteden.
Elk uur vaart er vanuit beide havens een schip uit. De reis duurt precies 7 uren
en een schip blijft 1 uur in de haven liggen voor het laden en lossen.
Hoeveel schepen zijn minimaal nodig?
Hoeveel schepen kom je tijdens de reis op volle zee tegen?
Neem eens aan, dat de reis precies T uren duurt.
Stel dan formules op voor bovenstaande vragen.
27. Draaicirkel.
Onder de wielbasis W verstaan we de afstand tussen de assen van het voor- en het
achterwiel van een auto, fiets enz.
Stel eens, dat het voorwiel een hoek van a graden maakt met het achterwiel.
Stel een formule op voor de straal R van de draaicirkel.
28. Wegennet
Vier dorpjes liggen op de hoekpunten van een vierkant dat zijden van 10km. heeft.
Bereken de minimale afstand van een wegennet, dat die dorpjes met elkaar verbindt.
29. Brulboei.
Een brulboei loeit 5 keer in 52 seconde en 8 keer in 88 seconde.
Bereken de tijd waarin de boei 10 keer loeit.
30. Robot.
Een robot voert 5 keer achtereen de volgende 2 handelingen uit:
1. beweeg een vaste afstand vooruit
2. draai over een vaste hoek naar rechts
Daarna staat de robot weer in zijn uitgangspositie.
Over welke hoek draaide de robot elke keer?
31. P berekenen.
Een stuk karton van a x a cm2 weegt A gram.
Een cirkel met straal r, uit hetzelfde karton geknipt,
weegt R gram.
Bedenk een formule, waarmee je p kunt berekenen
als a, A, r en R door meting en weging bekend zijn.
32. Een vreemd getal.
Een getal eindigt op het cijfer 2.
Als deze 2 van de rechter- naar de linkerkant van het getal wordt
verplaatst ontstaat een nieuw getal, dat twee keer zo groot is
als het oorspronkelijke.
Wat is het kleinste getal met deze eigenschap?
33. Lichtstraal.
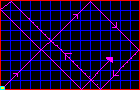 Rechts zie je het bovenaanzicht van een kamer met spiegelende wanden.
Rechts zie je het bovenaanzicht van een kamer met spiegelende wanden.Een lichtbron zendt een straal uit.
Hoeveel hokjes moet de straal doorkruisen om weer bij de lichtbron uit te komen?
Hoeveel hokjes moet de straal doorkruisen als de kamer a x b hokjes meet?
34. Vierkant.
Van rechthoekige tegels van 24 x 39 cm2 moet een zo klein
mogelijk vierkant worden gelegd.
Hoeveel tegels zijn hier minimaal voor nodig?
En hoeveel tegels zijn nodig als een tegel a x b cm2 meet?
35. Gemiddelde klassengrootte.
Pedagogen stellen, dat de leerprestaties beter zijn bij kleinere schoolklassen.
Het "van Speyk" college adverteert, dat het gemiddeld zeer kleine klassen heeft.
Er zijn namelijk 10 klassen van 2 leerlingen en 2 klassen van 50 leerlingen.
Bereken de gemiddelde klassengrootte.
Vanuit de leerling bekeken is dit gemiddelde niet erg realistisch.
Beter zou het zijn aan elke leerling afzonderlijk te vragen naar het aantal
klasgenoten, die leerling zelf meegerekend.
Welke berekening geeft de situatie dus beter weer?
36. Stelling 1.
Als twee driehoeken een gelijke hoek hebben, dan verhouden hun
oppervlakten zich als het product van hun zijden om die hoek.
Is deze stelling juist? Zo ja, geef het bewijs.
Zo nee, geef een tegenvoorbeeld.
37. Stelling 2.
Van elke driehoek geldt, dat elke zijde korter is dan de halve omtrek.
Is dit juist? Zo ja, lever het bewijs.
Zo nee, geef een tegenvoorbeeld.
38. Constructie 1.
Van een driehoek zijn gegeven:
- de lengte van de basis
- een basishoek
- de som van de lengtes van de opstaande zijden
Hoe verloopt de constructie?
Gebruik passer en liniaal of geodriehoek.
39. Constructie 2.
Van een driehoek zijn gegeven:
- de lengte van de basis
- een basishoek
- het verschil van de lengtes van de opstaande zijden
Hoe verloopt de constructie?
Gebruik passer en liniaal of geodriehoek.
40. Bootje.
Een bootje vaart met een snelheid van 12km/h over het water.
Eerst wordt vanuit de haven een rivier 7 uur stroomopwaarts bevaren.
Daarna draait de kapitein om en na 2 uur varen wordt de haven weer bereikt.
Bereken de stroomsnelheid van de rivier.
41. Examen.
Bij een examen kunnen de kandidaten totaal 72 punten verdienen.
Elk punt telt evenveel mee voor het cijfer. Minimaal wordt het
cijfer 1 en maximaal het cijfer 10 toegekend.
Welke formule kan je gebruiken om uit het aantal punten
p het cijfer c te berekenen?
Na het examen blijkt een opgave een fout te bevatten.
Deze opgave leverde maximaal 6 punten op, maar geen enkele kandidaat
heeft een punt behaald. Besloten wordt, deze opgave niet voor het
cijfer te laten meetellen.
Met welke formule kan je het gecorrigeerde cijfer k uit het oude
cijfer c berekenen?
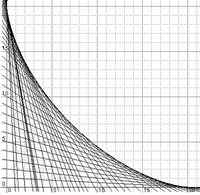 42. LadderCurve.
42. LadderCurve.De curve hiernaast is ontstaan, door een ladder van
10 meter met de ene kant over de grond en met de andere
kant tegen een muur op te rollen.
Stel de vergelijking op van deze curve.
(verrassend fraai!)
43. Expeditie.
Een expeditie trekt van dorp P dieper het oerwoud in naar het 10km. verder
gelegen Q. Verder van P wordt het woud dichter en vordert de expeditie langzamer.
De formule v = 5 - 0,4.a geeft de snelheid aan op afstand a van P.
Hoe lang duurt de tocht van P naar Q?
44. Telefoon.
Een telefoonnummer in een dorpje is 4 cijfers lang.
Een '0' als eerste cijfer maakt een verbinding buiten het dorp.
Hoeveel toestellen kunnen maximaal binnen het dorp worden aangesloten?
De bewoners blijken grote problemen te hebben met telefoneren.
Regelmatig wisselen ze cijfers om, waardoor een verkeerde verbinding
tot stand komt.
De telefoonmaatschappij besluit hier wat aan te doen: de centrale wordt
zo ingericht, dat bij verwisseling van de cijfers toch de goede verbinding
wordt gemaakt.
Hoeveel toestellen kunnen nu maximaal binnen het dorp worden aangesloten?
45. Olievat.
 Een olievat met diameter D en lengte L ligt op zijn kant.
Een olievat met diameter D en lengte L ligt op zijn kant.(zie tekening)
Met een peilstok kan de inhoud van het vat worden gemeten.
Bedenk een formule, waarmee je de inhoud kunt uitrekenen
door de peilstok af te lezen.
opmerking: misschien is het handig van een half gevuld vat uit te gaan,
de peilstok wijst dan -0- aan. Reken later terug naar echte peilhoogte.
46. Piramide.
Met een zaagbank kunnen planken op maat worden gezaagd. Het zaagblad is van
0 tot 45 graden instelbaar. Bij 0 graden wordt een plank recht (90 graden)
afgezaagd, bij bv. een instelling van 10 graden krijgt de plank een hoek van
80 graden aan de ene- en 100 graden aan de andere kant.
Een kunstenaar wil een aantal piramides bouwen. Als grondvlak neemt hij een
vierkant met zijde B cm. De top ligt H cm. boven het grondvlak.
De vier zijden zijn gelijk van vorm.
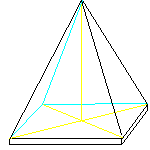
Bedenk formules voor de afmetingen van een zijde.
Bereken de instellingen van de zaagbank om de zijvlakken van de juiste hoeken
te voorzien.
47. Maanbasis.
Over een aantal jaren zal er op de maan een basis zijn met ruimtehaven.
Raketten verzorgen het verkeer met de aarde.
Soms raakt een raket uit de koers en landt op enige afstand van de haven.
Dan moet een reddingsoperatie plaatsvinden. Dat wordt gedaan met een MTV,
Maan Transport Vehikel. Een MTV wordt aangedreven door brandstofstaven.
Er is plaats voor 4 staven, 1 in bedrijf en 3 reserve. Om veiligheidsredenen mag
alleen een geheel uitgewerkte staaf door een nieuwe worden vervangen.
Op 1 staaf kan 50km. worden afgelegd. De basis heeft een grote voorraad staven.
Een extra probleem treedt op, als een raket meer dan 100km. uit de koers is geraakt.
Dan moet de MTV onderweg eerst voorraden brandstofstaven aanleggen
om de reddingsactie te kunnen voltooien.
Ga uit van reddingsacties op afstand 50,100,150,200 etc. km.
Bedenk een formule, die aangeeft hoeveel brandstofstaven een reddingsoperatie
kost bij een gegeven afstand.
48. Treintjes.
 Twee treintjes moeten elkaar op enkelspoor passeren.
Twee treintjes moeten elkaar op enkelspoor passeren.Zie tekening voor bovenaanzicht.
Op de draaischijf kunnen twee wagons staan.
Door 180 graden te draaien verwisselen die wagons van plaats.
Als de treintjes elk uit 3 wagons bestaan, hoeveel -halve- omwentelingen
zijn dan nodig voor het passeren?
Stel, dat het ene treintje uit A en het andere uit B wagons bestaat, hoeveel
-halve- omwentelingen zijn dan nodig?
49. Deelbaar door 17?
Waar of onwaar? Als voor twee gehele getallen x en y
2x + 3y deelbaar is door 17, dan is ook 9x + 5y deelbaar door 17.
50. De vriendelijke familie
Volgende week is het dan zover:
het liefhebbende echtpaar Hendrikus Haat en Cornelia Haat-Nijd is 40 jaren
getrouwd.
De familie organiseert een groot feest, met oa. een diner in restaurant
"Koek en Ei" en een tocht in Oldtimers.
Zoon Jacobus heeft 3 wagens gehuurd voor de 10 feestgangers.
Elke wagen biedt plaats aan maximaal 4 familieleden.
Er is echter nog een probleempje: hoe moet de familie over de wagens
worden verdeeld, want:
- Hendrikus en kleine Kees haten Marianne
- Jacobus, Willem en oom Gerard pesten Hendrikus
- Marianne wil niet, dat haar man Jacobus in dezelfde wagen zit
als de beeldschone Jolanda
- Willem haat oom Gerard en kleine Kees
- Hendrikus, Jolanda en kleine Kees worden niet goed van het parfum
van tante Ella
- Cornelia maakt Jolanda en Marianne gek met haar geroddel
- Frederik haat Marianne, Cornelia en Hendrikus
- Cornelia pest kleine Kees
Hoe moeten de wagens worden ingedeeld voor een geslaagde rijtoer?
51. De schudrobot
Een uitvinder heeft een robot bedacht, die speelkaarten schudt.
Het apparaat kan uiterst nauwkeurig worden ingesteld. Bij elke instelling
hoort een vaste verwisseling van de kaarten.
Als de oorspronkelijke volgorde aangegeven wordt met [1,2,3,4,5,......]
en na het schudden is die [5,7,3,1,9....] dan betekent dat, dat kaart 5 nu boven ligt
met daaronder kaart 7 terwijl kaart 3 op zijn plaats is blijven liggen.
Stel, dat voor 52 speelkaarten de volgende instelling actief is:
[1,27,2,28,3,29,............26,52]
1.Na hoeveel keer schudden liggen de kaarten weer in hun oorspronkelijke volgorde?
2.Hoeveel instellingen van de robot zijn mogelijk met 52 speelkaarten?
3.Wat is het maximaal mogelijke aantal schuddingen waarna de 52 kaarten weer
in hun oorspronkelijke volgorde liggen?
52. Duizenden
De dag voor de vakantie heb ik dit spelletje vaak gespeeld in de onderbouw van
het V.O. Het gaat als volgt:
Elke leerling tekent een vierkant van 3 * 3 vakjes.
Leerlingen gooien om beurten met een dobbelsteen en noteren de uitkomst in
een vakje naar keuze. (dobbelsteen in jampot met vastgeplakte deksel)
Na 9 worpen zijn alle vakjes gevuld. Elke rij wordt nu beschouwd als een getal
van 3 cijfers en die getallen worden opgeteld.
Elke leerling, die een uitkomst heeft in het interval 992..1008 scoort
een punt. Wie precies 1000 heeft krijgt 3 punten.
Na een afgesproken tijd is de winnaar degene met de meeste punten.
1.Wat is de gemiddelde uitkomst bij willekeurig invullen?
2.Bewijs dat het verschil van twee uitkomsten altijd een veelvoud is van 9.
(zo betrap je valsspelers)
3.Bedenk een strategie om de kans op winst te vergroten.
53. Veelvoud
De som van n opvolgende (gehele) getallen is een veelvoud van n.
Onder welke voorwaarde(n) van n is deze bewering juist?
54. Tegels
Dit is een zg. 2*2 tegel: op elke zijde komen
twee verschillende wegen uit.
Als tegels, zonder verdraaiing, worden
neergelegd en er ontstaan rondgaande wegen,
dan noemen we zo'n tegel een "circuit-tegel".
vier tegels lang is.
We vragen ons af, of er circuit-tegels
bestaan met grotere circuit-lengte.
En welke lengtes er dan mogelijk zijn.
1.
Ontwerp een tegel met circuit-lengte 8.
2. Kan een tegel met circuit-lengte 5
bestaan?
3.
Wat is het grootste circuit, dat met
een n * n tegel mogelijk is?
55.Veren
 |
Die geeft aan, hoeveel kg. kracht er nodig is om de veer 1cm. uit
te rekken. (natuurkundigen rekenen in Newton en meters)
In formule: C = K / u waarbij:
C: de veerconstante
K: de kracht in kg.
u: de uitrekking in cm.
Op het plaatje hiernaast zie je een veer, die bestaat uit twee in serie
bevestigde veren met veerconstanten van 2 en 3 kg/cm.
a. Bereken de veerconstante van de gehele veer.
b. Bedenk een formule voor de veerconstante C van een veer,
die bestaat uit in serie bevestigde veren met veerconstanten
C1, C2, C3...
56.Rotatie
Teken twee lijnstukken AB en A'B' van dezelfde lengte.
Zorg ervoor, dat A'B' geen evenwijdige verschuiving is van AB.
Laat zien, dat A'B' de rotatie is van AB en bepaal het rotatie-middelpunt.
57.Verschuiving
Waar of onwaar?
Een evenwijdige verschuiving van een lijnstuk kan ook worden bereikt met
twee achteenvolgende lijnspiegelingen.
58.Vereenvoudig deze formule
|
59.Marathon
Tien ploegen van elk zeven atleten nemen deel aan een marathon.
Onder de rangorde van een atleet verstaan we de volgorde waarin hij
over de eindstreep gaat (1,2,3...). Geen twee atleten finishen gelijktijdig.
De rangorde van een ploeg is de som van de rangorden van zijn atleten.
wat is de hoogste rangorde waarvoor een ploeg nog zeker winnaar is?
60.Trappen klimmen
Een trap kan met 1 of 2 treden tegelijk worden beklommen.
Een trap met 1 trede kan dus op 1 manier worden beklommen: (1).
Een trap met 2 treden kan op 2 manieren worden beklommen: (11, 2).
Een trap met 3 treden kan op 3 manieren worden beklommen: (111,12,21).
Op hoeveel manieren kunnen trappen met 4,5,6,7...treden worden beklommen?
61.Hoeveel deelnemers?
Een congres wordt bezocht door Amerikanen, Europeanen en Aziaten.
Hun aantallen verhouden zich als 10 : 17 : 23.
Ook is bekend, dat er 138 meer Aziaten dan Europeanen aanwezig zijn.
Wat is het totale aantal deelnemers?
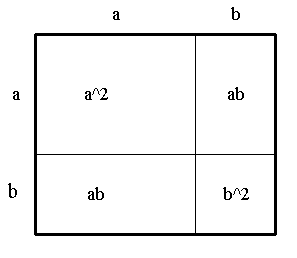
62.Merkwaardige Producten
Zo worden de volgende producten genoemd:
 |
-
(a + b)2 = a2 + 2ab + b2
(a - b)2 = a2 - 2ab + b2
(a - b)(a + b) = a2 - b2
Bedenk ook afbeeldingen van de andere merkwaardige producten.
63.Ackermann functie
Exponentiële functies kunnen hard oplopen, maar het kan nog veel erger.
Stel eens, dat voor een functie f(x,y) geldt: (natuurlijke getallen)
f(0,y) = y + 1
f(x+1,0) = f(x,1)
f(x+1,y+1) = f(x, f(x+1,y))
Bereken:a) f(1,1)
b) f(2,2)
c) f(3,3)
d) bedenk formules voor f(1,p) , f(2,p) , f(3,p)
64.Driehoek
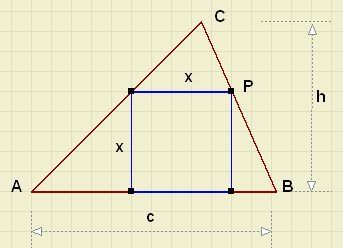 Binnen een willekeurige scherphoekige driehoek
Binnen een willekeurige scherphoekige driehoekis een vierkant getekend, waarvan de hoekpunten
op de zijden liggen.
1. Hoe moet punt P worden geconstrueerd? (met passer en liniaal).
2. Bedenk een formule voor x als h en c bekend zijn.
65.Cirkel
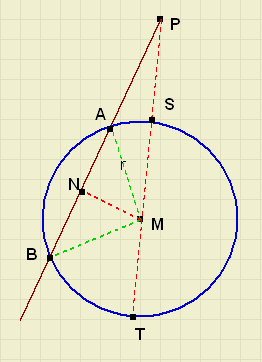 In de figuur rechts is P een vast punt.
In de figuur rechts is P een vast punt.Een willekeurige lijn door P snijdt de cirkel in A en B.
Opmerkelijk: het product PA.PB lijkt steeds een constante waarde
te bezitten, onafhankelijk van de ligging van A en B,
dus slechts afhankelijk van de straal r van de cirkel
en de positie van P.
Bewijs dat dit zo is.
Opmerking: dit product heet de macht van P t.o.v. de cirkel.
66. de Galaxianen
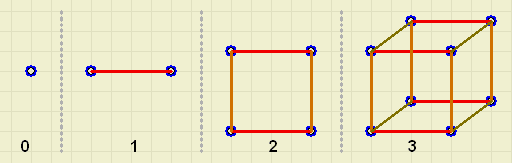
In een ver verwijderd zonnenstelsel leven de Galaxianen.
Lang geleden begonnen zij de ruimte te koloniseren vanuit 1 stad (0 dimensies).
Een eeuw later bestond hun rijk uit 1 dimensie: 2 steden en 1 weg.
Na twee eeuwen was hun rijk uitgebreid tot 2 dimensies: 4 steden, 4 wegen.
Weer een eeuw later waren 3 dimensies voltooid: 8 steden, 12 wegen.
Zo bouwden zij onvermoeibaar, eeuw na eeuw, voort.
Hoeveel steden en wegen waren er in 4 dimensies?
En in 5,6,7....dimensies?
Bedenk formules voor het aantal steden en wegen in n dimensies.
67. Welke hoek?
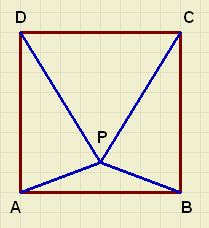 Hiernaast zie je vierkant ABCD met daarin
Hiernaast zie je vierkant ABCD met daarinde gelijkzijdige driehoek PCD.
Bereken hoek PAB.
68. Het Wilde Westen
Reizen in het Wilde Westen was niet zonder gevaar.
De reiziger kon door bandieten worden overvallen,
in een ravijn storten, door grizzly beren worden geconsumeerd,
of gewoon verdwalen en omkomen van honger en dorst.
Hieronder zie je een oude landkaart van een berucht gebied.
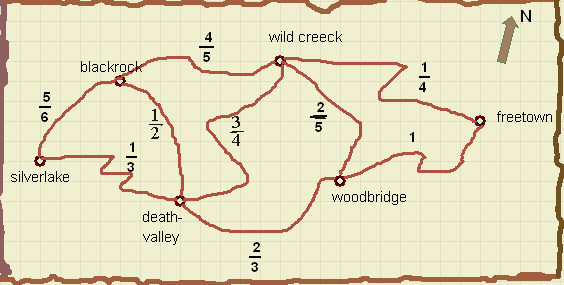
Bij elk traject staat de overlevingskans aangegeven.
Een kans van 2/3 (tweederde) betekent, dat slechts 2 van de 3 reizigers aankomen.
Bij een kans van 1 komt elke reiziger goed aan.
Bepaal de minst gevaarlijke route van Silverlake naar Freetown.
Hoe groot is de overlevingskans?
69. Parket leggen
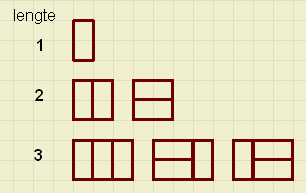 Een gang met breedte 2 wordt belegd met stukken parket met afmeting 1*2.
Een gang met breedte 2 wordt belegd met stukken parket met afmeting 1*2.Als de gang lengte 1 heeft, dan is er maar 1 manier van beleggen mogelijk.
Bij een gang van lengte 3 zijn er 3 manieren mogelijk.
Op hoeveel manieren kan een gang van lengte 4, 5, 6, .... worden belegd?
70. Het Geboortejaar
Op nieuwjaarsdag van het jaar 1997 ontmoet de heer Zwart, een wiskundeleraar,
een vroegere leerling, mevrouw de Wit.
De Wit merkt op, dat zij net zo oud is als de som van de cijfers van haar geboortejaar.
Zwart denkt even heel diep na en zegt dan: "van harte gefeliciteerd met je verjaardag!"
Hoe oud is mevrouw de Wit?
Hoe kan Zwart weten, dat zij vandaag jarig is?
Opmerking: schrijf een computerprogrammatje om dit probleem op te lossen.
71. Rekentruc
Neem een getal van 3 cijfers in gedachten. (Het eerste cijfer moet groter zijn dan het derde)
Noem dit getal 1.
Verwissel het eerste en derde cijfer. Noem dit getal 2.
Trek getal 2 af van getal 1. Noem dit getal 3.
Verwissel het eerste en derde cijfer van getal 3. Noem dit getal 4.
Tel getal 4 op bij getal 3.
Herhaal dit voor een paar getallen.
Wat valt op?
Bewijs deze eigenschap.
72. Communicerende vaten
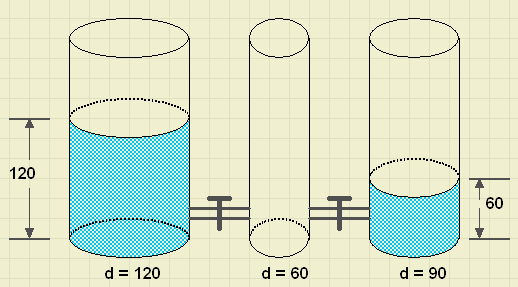
In het plaatje hierboven zie je drie cilindervormige vaten waarvan
er twee gedeeltelijk met water zijn gevuld.
De kranen staan dicht.
Waterhoogten en diameters van de vaten staan aangegeven.
Bereken de waterhoogte in de vaten nadat de 2 kranen zijn geopend.
73. Het Kettinkje
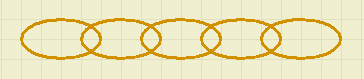 Janneke heeft 6 stukjes van een kettinkje.
Janneke heeft 6 stukjes van een kettinkje.Elk stukje heeft 5 schakeltjes.
Van de losse stukjes wil zij een gesloten ketting laten maken.
Een edelsmit rekent 50 cent voor het losmaken van een schakeltje en 1,25
voor het dichtsolderen van een schakeltje.
De rekening van de edelsmit bedraagt 8,75
Hoe is de smit te werk gegaan?
74. De Verdwenen Streep
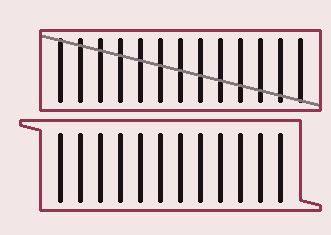 Rechts zie je twee plaatjes van een bordje met strepen.
Rechts zie je twee plaatjes van een bordje met strepen.Het bovenste bordje is schuin doorgeknipt.
Het onderste plaatje toont het bordje, maar dan verschoven.
In het onderste plaatje ontbreekt een streep, hoe is dat mogelijk?
75. Roosters lassen (2d)
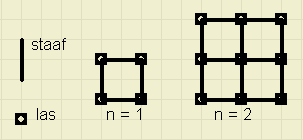 Van rechte staven worden platte rooster gelast.
Van rechte staven worden platte rooster gelast.
Hoeveel lassen en hoeveel staven heeft rooster 3, 4, 5, ....
Bedenk een formule voor het aantal lassen en staven van rooster n.
76. Roosters lassen (3d)
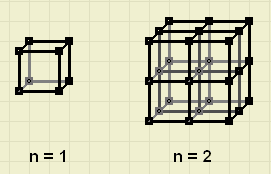 Van rechte staven worden kubusvormige constructies gelast.
Van rechte staven worden kubusvormige constructies gelast.
Bedenk formules voor het aantal lassen en staven van kubus n.
77. Draden tellen
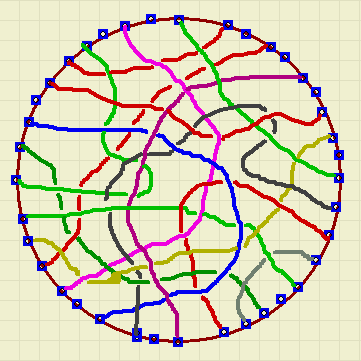 Op het plaatje rechts zie je een kluwen van draden.
Op het plaatje rechts zie je een kluwen van draden.
Hoeveel draden zijn het?
Wat is een handige manier om het aantal vast te stellen?
78. priemgetallen
P is een priemgetal en p > 3.
k is een natuurlijk getal, k = 1,2,3,4,......
a. Toon aan, dat p geschreven kan worden als p = 6k - 1 of als p = 6k + 1
b. Gebruik bovenstaande regel en toon aan, dat p2 - 1 deelbaar is door 24.
79. Rugzak
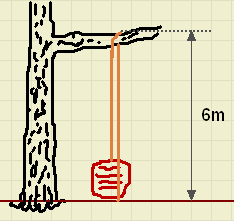
Kampeerders in de Rocky Mountains moeten 's nachts hun rugzakken in een boom
hangen tegen nieuwsgierige grizzly beren.
Zie de twee plaatjes hieronder.
 |
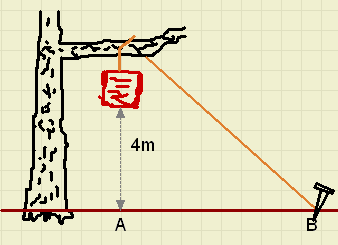 |
Bereken de afstand AB.
80. Bevolking
In een land wil de regering de overbevolking tegengaan door gezinnen
maar één kind toe te staan.
Maar omdat de bevolking een sterke voorkeur heeft voor jongetjes, wordt de
maatregel iets verzacht: na het eerste jongetje in een gezin mogen er geen
kinderen meer bijkomen.
Hoe zal de bevolkingssamenstelling er na verloop van tijd uitzien?
81. Bereken
Als x/y = 21, bereken dan:
- (x+y)/(x-y)
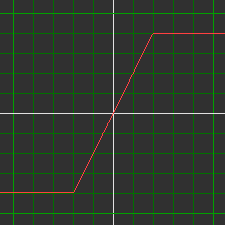
82. Geknikte functies
 |
 |
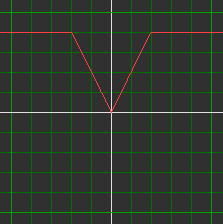 |
De formule van de linkse grafiek heeft de vorm ...x...y... = ...
en de andere twee y = ...x....
De grafieken zijn getekend met het programma "Graphics Explorer", freeware op deze website.
- Bedenk de formule bij elke grafiek.
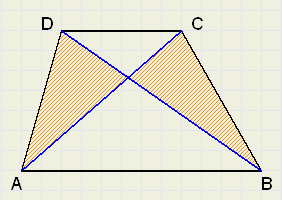 |
ABCD is een trapezium, omdat AB||CD.
Beredeneer dat de gearceerde oppervlakten gelijk van grootte zijn.
84. Wortel 2
Bereken met je rekenmachine de wortel uit 2.
Schrijf dit getal op.
Kwadrateer het antwoord en de 2 is terug.
Wis het schermpje van je rekenmachine en tik het opgeschreven getal in.
Kwadrateer het en hé, het antwoord is niet 2 maar 1.999999999
Geef een verklaring hiervoor.
85. Pompen
Pomp 1 pompt een zwembad leeg in 8 uur.
Pomp 2 heeft hier maar 6 uur voor nodig.
hoeveel tijd is nodig als pompen 1 en 2 samenwerken?
86. Zagen
Een zaag heeft een dikte van 3 mm.
Met deze zaag wordt een rechthoekige plank in 10 gelijke stukken gezaagd.
Daarbij treedt een verlies op van 1%.
a. hoe lang is elk afgezaagd stuk?
b. wat is het rendement (deel dat niet verloren gaat) als een plank van L meter
in n gelijke delen wordt gezaagd en het zaagblad een dikte heeft van d mm?
 87. Verhouding
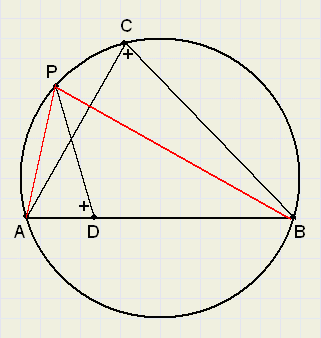
87. VerhoudingZie figuur.
Gegeven is DABC met omgeschreven cirkel en AD : DB = 1 : 3
LADP = LACB
Bereken de verhouding PA : AB en PD : PB
 88. de Prinses en de Draak
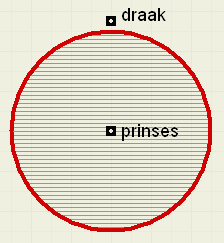
88. de Prinses en de DraakDit is een klassiek probleem, maar daarom niet minder aardig.
Een prinses bevindt zich midden in een cirkelvormige vijver en moet ontsnappen
aan een draak,die aan de kant staat.
De prinses is op het land sneller dan de draak, die niet te water gaat maar sneller loopt
dan de prinses kan zwemmen.Zie figuur.
Hoe kan de prinses ontsnappen?
Welke verhouding (zwemsnelheid prinses) : (loopsnelheid draak) is
hiervoor minimaal nodig?
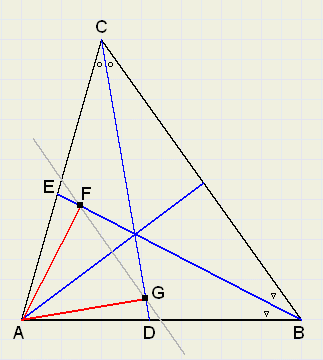 89. Evenwijdig.
89. Evenwijdig.In de figuur hiernaast
-
- is CD deellijn van hoek C
- is BE deellijn van hoek B
- staat AF loodrecht op BE
- staat AG loodrecht op CD
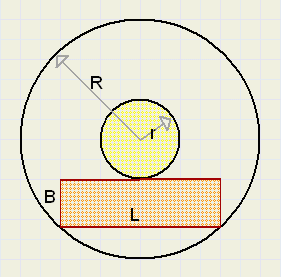 90. Vlot in vijver.
90. Vlot in vijver.In de figuur hiernaast zie je een vijver (straal R) met daarin een eiland (straal r).
Het vlot heeft een lengte L en past precies in de vijver.
Vind een formule voor de breedte B van het vlot, uitgaande van L,R,r
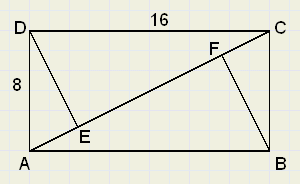 91. Rechthoek.
91. Rechthoek.In rechthoek ABCD zijn vanuit B en D
loodlijnen BF en DE getrokken op diagonaal AC.
Bereken de lengte van EF.
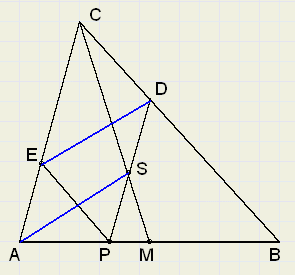 92. Parallellogram.
92. Parallellogram.Gegeven is DABC met M op midden AB
P willekeurig op AB.
PD || AC en PE || BC
Bewijs, dat ASDE een parallellogram is.
 93. Hanoi
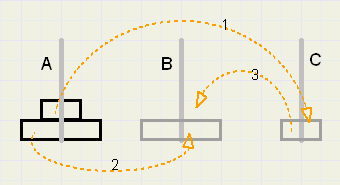
93. HanoiDe torens van Hanoi.
Dit is een klassiek probleem, maar daarom nog best leuk.
Een stapel schijven moet worden verplaatst, waarbij de regel geldt
dat een schijf nooit op een kleinere mag liggen.
Geen twee schijven zijn gelijk van grootte.
Alleen de bovenste schijf van een stapel kan verplaatst worden.
Tijdelijk mag één extra stapel (C) worden gemaakt.
De verplaatsing van een stapel van 2 schijven (A naar B) verloopt aldus:
- bovenste schijf van A naar C
- schijf van A naar B
- schijf van C naar B
zodat er totaal 3 verplaatsingen nodig zijn.
Hoeveel verplaatsingen zijn nodig voor een stapel (A naar B) van 3,4,......, n schijven?
 94. Pion1
94. Pion1Een pion wordt door twee spelers om beurten 1,2, of 3
hokjes naar links verplaatst.
Winnaar is degene die de pion in vakje -0- zet.
De pion staat op vakje 85 en je bent aan zet.
Welke zet doe je?
 95. Pion2
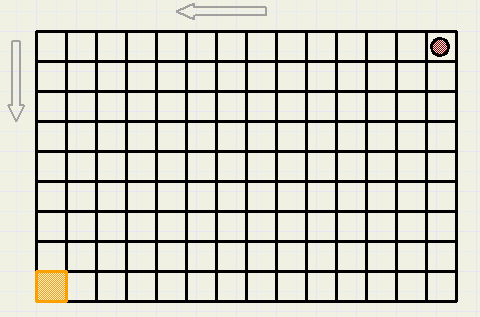
95. Pion2Twee spelers verzetten om beurten een pion op een bord.
Per zet mag de pion naar links (binnen een rij) of omlaag
(binnen een kolom) worden verplaatst , net zoveel hokjes als mogelijk is.
Winnaar is degene die de pion in het gekleurde hokje linksonder plaatst.
De pion staat als hiernaast aangegeven en je bent aan zet.
Welke zet doe je?
Welke zet moet je doen, als de pion ook diagonaal links omlaag
gezet mag worden?
 96. Curve
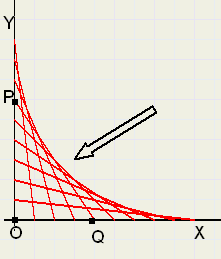
96. CurveDe grafieken hiernaast zijn onstaan door steeds lijnen PQ te trekken,
zodanig dat OP + OQ = 10.
(P op y-as, Q op X-as).
Stel de vergelijking op van de curve die je ziet ontstaan als je steeds meer lijnen trekt.
97. Knuffelberen
Kleine Annelies heeft in een grote doos 10 zwarte, 20 gele en 40 bruine knuffelberen.
Zonder te kijken pakt ze wat beren uit de doos en zet ze op een rijtje.
Hoe lang moet die rij minstens zijn om zeker te weten dat
a. er minstens 1 gele bij is
b. er minstens 1 bruine bij is
c. er drie dezelfde bij zijn
d. er 13 dezelfde bij zijn
e. er ergens twee verschillende naast elkaar zitten
f. er ergens twee bruine naast elkaar zitten
g. er drie verschillende bij zijn
 98. Loodlijn
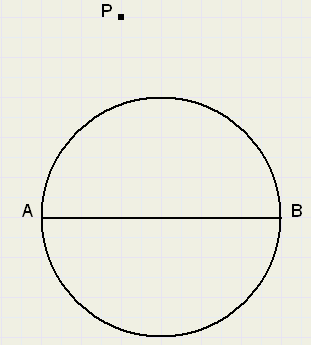
98. LoodlijnGegeven is een cirkel met zijn diagonaal AB en een punt P buiten de cirkel.
Construeer de hoogtelijn uit P op AB en gebruik daarbij alleen een liniaal.
99. Letters
Een student stuurt zijn ouders het volgende bericht in de vorm van een optelling:
S E N D |
M O R E |
M O N E Y |
Welk cijfer hoort bij elke letter?


