

| Regelmatige veelhoeken |
Dit artikel beschrijft ook
-
- berekening van het snijpunt van lijnen en cirkels
- theorie van puntrotatie
- een vergrootglas voor bitmaps
Introductie
Hieronder staan wat regelmatige veelhoeken (met 3 tot 8 hoeken):
Een regelmatige N-hoek is te beschouwen als N identieke gelijkbenige driehoeken
met als top een hoek van 360/N graden.
Dit Delphi project komt voort uit een meetkunde probleem.
Gevraagd is in de onderstaande figuur hoek x te berekenen.
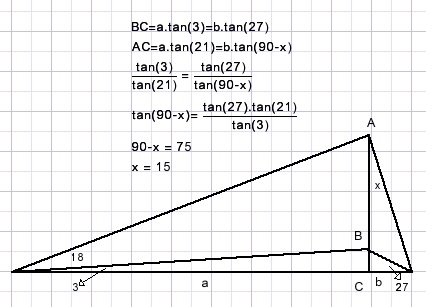
De getoonde algebra´sche oplossing vereist het gebruik van een rekenmachine.
Meetkunde problemen worden eleganter opgelost door toepassing van eerder afgeleide stellingen
en logisch redneren. Een meetkundifge oplossing voor dit probleem lijkt moeilijk totdat we opmerken
dat alle hoeken een veelvoud van 3 zijn.
Hoeken van 3 graden op een cirkelboog omspannen een boog van 6 graden op die cirkel
volgens het theorema van Thales. (Grieks wiskundige, 500vChr.).
Na tekenen van de driehoek in een 60-hoekige regelmatige driehoek en omgeschreven cirkel
is de oplossing meteen zichtbaar. (zijden van de veelhoek zijn hier niet getekend).
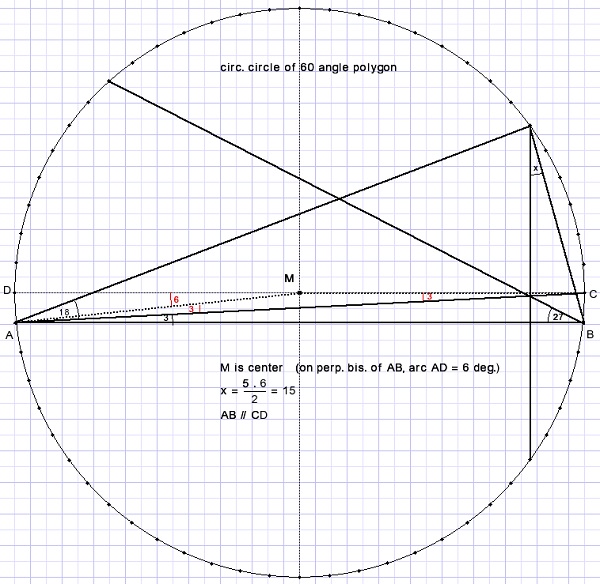
Een boog tussen twee punten telt 360/6 = 6 graden.
X omspant een cirkelboog van 5*6 graden dus x = 30/2 = 15 graden.
Een aanpak als deze is in meer gevallen handig.
Vandaar dit kleine project om regelmatige veelhoeken te tekenen en te onderzoeken.
Intermezzo (1)
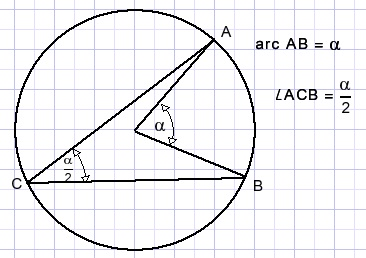
Hoeken zijn te meten met cirkelbogen.In het volgende plaatje is boog AB α graden, dat is de bijbehorende middelpuntshoek.
Volgens het theorema van Thales is een hoek op een cirkel (zoals C) de helft van de bijbehorende boog (AB).
Het bewijs staat hier.
Het project
Hieronder staat een iets verkleinde afbeelding van het programma in bedrijf.Getoond wordt een regelmatige 18 hoek met diagonalen en omgeschreven cirkel.
Gekleurde punten zijn snijpunten van diagonalen, de kleur geeft het aantal snijdende diagonalen aan.
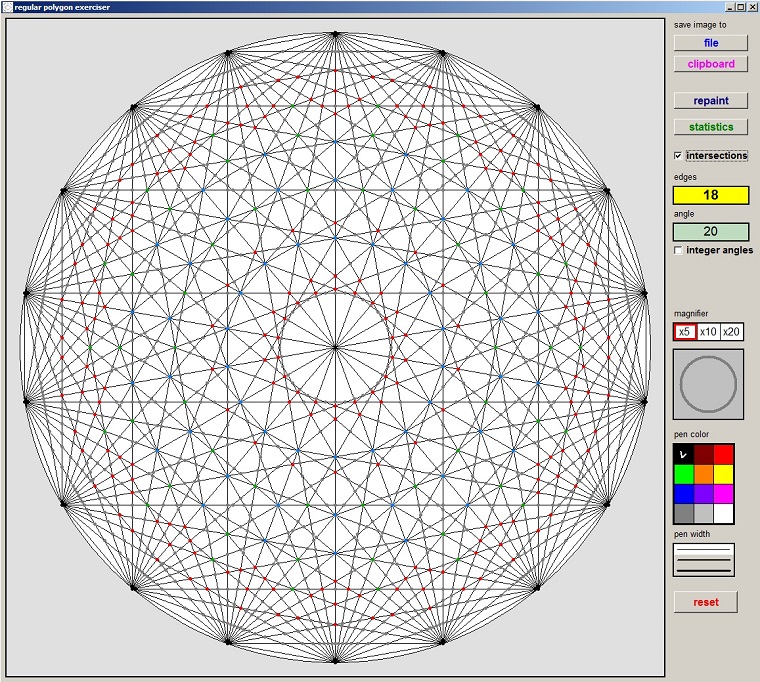
De knoppen bewerkstelligen:
-
- Plaatje opslaan in bestand of clipboard
- Hoek selectie (3 tot 60)
- Statistiek: aantal diagonalen, aantal lijnen per snijpunt
- Gekleurde lijnen tekenen met bepaalde pendikte
- Een vergrootglas over het beeld schuiven om snijpunten te onderzoeken
Ook over het programmeren van het vergrootglas.
Daarbij kan de lezer ook nog zijn middelbare school wiskunde opfrissen.
Hoeken selectie
De knop hiervoor is een TLabel component, om eens iets anders te doen.Tlabel heeft OnEnter en OnLeave events, daarmee is de achtergrondkleur te veranderen bij aktie.
procedure TForm1.Label1MouseEnter(Sender: TObject); begin label1.Color := $00c0ff; end; procedure TForm1.Label1MouseLeave(Sender: TObject); begin label1.color := $00ffff; end;Een linker-muisklik op het "edges" label verhoogt het aantal zijden, een rechter muisklik verlaagt het aantal.
Het eigenlijke werk wordt door een timer uitgevoerd, de TLabel events starten en stoppen de timer.
Voordeel daarvan is dat niet voortdurend met de muis geklikt hoeft te worden.
Ingedrukt houden volstaat.
Checkbox2.checked zorgt ervoor dat alleen gehele hoeken geselecteerd worden.
function IncEdges : boolean; //increment edgecount
var E : byte;
begin
if edgecount = maxEdge then result := false
else
begin
E := edgecount+1;
if form1.CheckBox2.checked then
while (E < maxEdge) and (360 mod E > 0) do inc(E);
setEdgecount(E);
result := true;
end;
end;
procedure setEdgeCount(newcount : byte);
const ff = '0.##';
begin
edgecount := newCount;
arc := 2*pi/edgecount;
tanArc := tan(arc); //values needed later
with form1 do
begin
label1.Caption := inttostr(edgecount);//show edgecount
label3.Caption := formatfloat(ff,360/edgecount);//show arc
end;
end;
Intermezzo (2)
Traditioneel worden hoeken gemeten in graden waarbij een hele omwenteling 360 graden bedraagt.Reden voor 360 is dat dit getal heel veel delers heeft.
Voor de berekening van sinus en cosinus is het handiger hoeken te meten in radialen.
360 graden komt overeen met 2 x π radialen, dat is de omtrek van een cirkel met een straal van 1.
Merk op, dat getal π altijd een benadering is. Er bestaat geen getal of breuk met precies de waarde π.
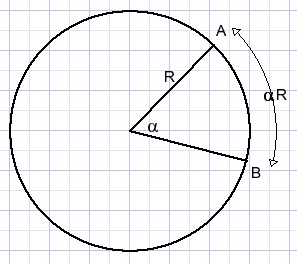
Een hoek van α radialen in het middelpunt van een cirkel met straal R staat op een boog (AB) van lengte αR.
Berekening van de hoeken
Tekenen gebeurt in een bitmap van 1001 * 1001 pixels.Expres een oneven getal omdat dan het punt [500,500] precies het midden is.
De omgeschreven cirkel heeft [500,500] als middelpunt, de straal telt 480 pixels.
Na tekenen wordt de bitmap zichtbaar door die naar paintbox1 op form1 te kopiŰren.
Bij een bitmap heeft de linkerbovenhoek co÷rdinaten [0,0].
Bij het tekenen komen we daar niet onderuit.
Maar bij berekeningen is het soms handiger het midden als oorsprong [0,0] te beschouwen.
Beide methodes worden hier toegepast.
Snijpunten bereken vraagt precisie. Pixel co÷rdinaten kunnen alleen afrondingen zijn en zijn dus onnauwkeurig.
Daarom worden ook de floating point co÷rdinaten bewaard.
Na berekening wordt het antwoord op helen afgerond om te kunnen tekenen.
De co÷rdinaten van de hoekpunten worden bewaard in array Alist.
Alist[1] is the top, hoekpunten 2,3,4,.. tellen met de klok mee.
De floating point waardes in Alist[ ] zijn relatief t.o.v. het midden [500,500].
Const maxEdge = 60;
type TCpoint = record
x,y : word; //absolute pixel position
rx,ry : single; //real value relative to screen center
end;
var Alist : array[1..maxEdge] of TCpoint;//list of polygon angles
procedure Arc2XY(var x,y : single; a : byte);//a= 1,2ů.
//supply x,y coordinates of polygon angle
var na : single;
begin
na := arc*(a-1);
x := 480*sin(na);
y := 480*cos(na);
end;
Filling the Alist[ ] array:
var i : byte;
x,y : word;
rx,ry : single;
begin
for i := 1 to edgecount do
begin
arc2XY(rx,ry,i);
Alist[i].x := round(rx)+500;
Alist[i].y := 500-round(ry);
Alist[i].rx := rx;
Alist[i].ry := ry;//UP + DOWN - ; center relative
end;
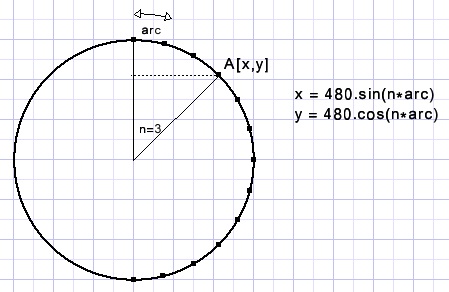
Voor details verwijs ik naar de source code.
Twee identieke bitmaps zijn in gebruik:
-
Map1 bevat de veelhoek en diagonalen.
Map2 is een kopie van map1 en voegt de gekleurde punten toe.
Ook worden in map2 tijdelijk lijnen getekend.
dat deel van map1 overheen te kopiŰren.
Gewijzigde delen van map2 worden na kopiŰren naar paintbox1 zichtbaar.
Hiermee vermijden we het wissen van de paintbox, wat hinderlijk geknipper zou opleveren.
Intermezzo (3)
Voor de berekening van snijpunten gebruik ik vector meetkunde.Hieronder staat de vector vergelijking van een rechte lijn (AB):
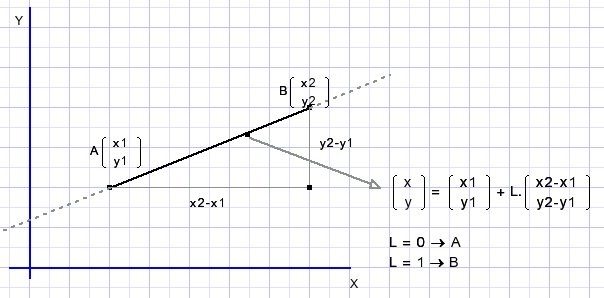
Naamgeving van variabelen: (zoals a1x):
//1 : beginpunt van de lijn 2: eindpunt van de lijn
//a :lijn door A. b : lijn door B
Berekening van het snijpunt van twee lijnen:
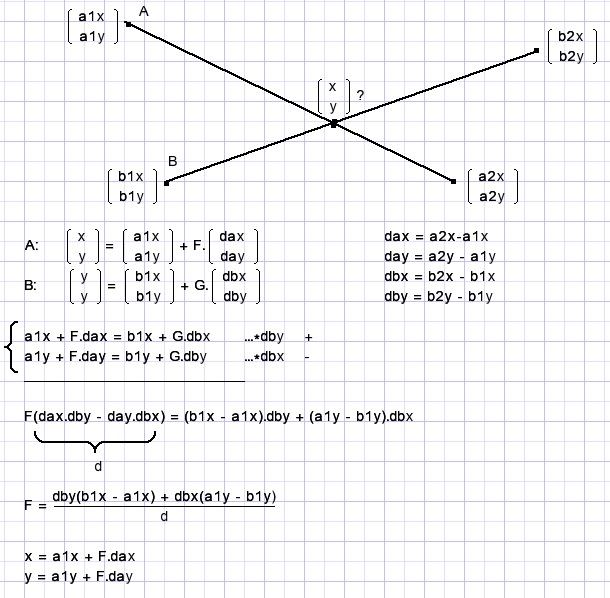
Programma
function GetIntersection(var x,y : single; a1,a2,b1,b2 : byte) : boolean; //return intersection (x,y) of diagonal a1-a2 and b1-b2 ; a1,2 b1,2 = 1,2,3ůAlist index //Return "false" in case of parallel lines (d = 0)Tijd besparen
Een regelmatige n hoek heeft n(n-1)/2 lijnen (zijden plus diagonalen).
Een regelmatige 60 hoek telt 1710 diagonalen.
Om de snijpunten daarvan te onderzoeken zouden dus 1.461.195 paar lijnen onderzocht moeten worden.
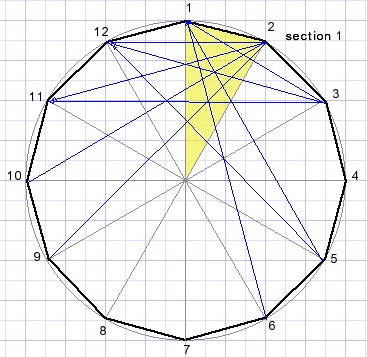
Dat kan sneller. Een regelmatige n hoek telt n gelijke segmenten. Er is rotatie symmetrie.
Alleen de snijpunten van sectie -1- berekenen is genoeg.
Met rotatie zijn dan de andere punten te bepalen.
const INSTlistmax := 10000;
type TIntersection = record
count : byte;
x,y : single;
end;
var INTSlist : array[1..INTSlistmax] of TIntersection;//list of intersections in section 1
De snijpunten worden toegevoegd aan array INTSlist. (intersections list)Als de x,y co÷rdinaten al in de lijst staan dan wordt alleen de waarde count verhoogd.
Intermezzo (4)
Punt rotatie.De positie van punt A(x,y) beschouwen we als de optelling van de afzonderlijke x en y ordinaten.
X en Y roteren we eerst onafhankelijk van elkaar, daarna tellen we de resultaten weer bij elkaar.
Rotatie is met de klok mee.
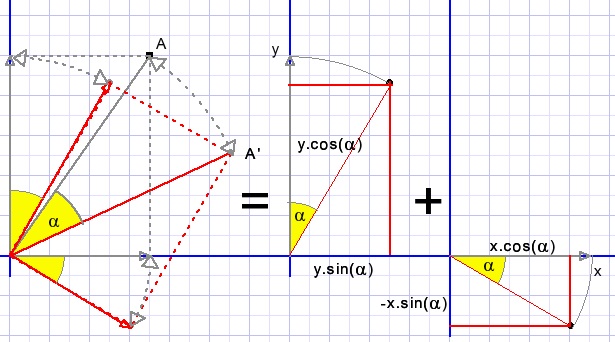
α is de rotatie hoek.
X wordt x.cos(α) en vermindert y met x.sin(α)
Y wordt y.cos(α) en verhoogt x met y.sin(α)
Opgeteld:
A(x,y) wordt A'(x',y') waarbij
X wordt x'= x.cos(α) + y.sin(α)
Y wordt y'= y.cos(α) - x.sin(α)
Procedure :
function GetDotColor(c : byte) : dword;
begin
case c of
2 : result := $808080; //grey
3 : result := $0000ff; //red
4 : result := $00b000; //dark green
5 : result := $ff8000; //blue
6 : result := $ffff00; //light blue
7 : result := $00c0ff; //orange
8 : result := $ff00ff; //purple
else result := $00000000; //black
end;//case
end;
procedure paintIntersections(sx,sy : single; count : byte);
//paint intersection point (sx,sy) of chords in all segments
//count : number of intersecting lines per point
var r : Trect;
x,y : word;
i : byte;
a,sina,cosa,rx,ry : single;
clr : dword;
begin
clr := getDotColor(count);
with map2.Canvas do
begin
pen.Color := clr;
brush.color := clr;
brush.Style := bsSolid;
for i := 0 to edgecount - 1 do
begin
a := i*unit1.arc;//not arc procedure but variable
sina := sin(a);
cosa := cos(a);
rx := sx*cosa + sy*sina;
ry := sy*cosa - sx*sina;
x := round(rx)+500;
y := 500-round(ry);
r := rect(x-2,y-2,x+3,y+3);
ellipse(r);
form1.PaintBox1.Canvas.CopyRect(r,map2.canvas,r);
end;//with
end;//for
end;
Het vergrootglas
Dat toont zijn deel van het plaatje 2, 5 of 10 keer vergroot.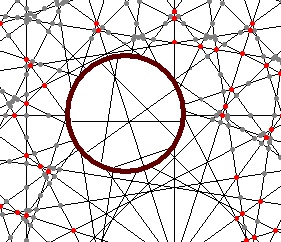
We bereiken dit door de co÷rdinaten van de hoeken tijdens berekening met m (2,5,10) te vermenigvuldigen.
Eigenlijk vindt geen vergroting plaats maar alleen herberekening van lijnen onder het vergrootglas.
De straal van het vergrootglas bedraagt 55 pixels.
Om berekening te vereenvoudigen wordt het midden van het vergrootglas als oorsprong van het gehele co÷rdinatenstelsel beschouwd.
Na berekeneing moeten de punten weer op hun plaats terugschuiven, dat spreekt.
Hieronder staat de gebruikte methode om de snijpunten van een lijn met een cirkel te berekenen.
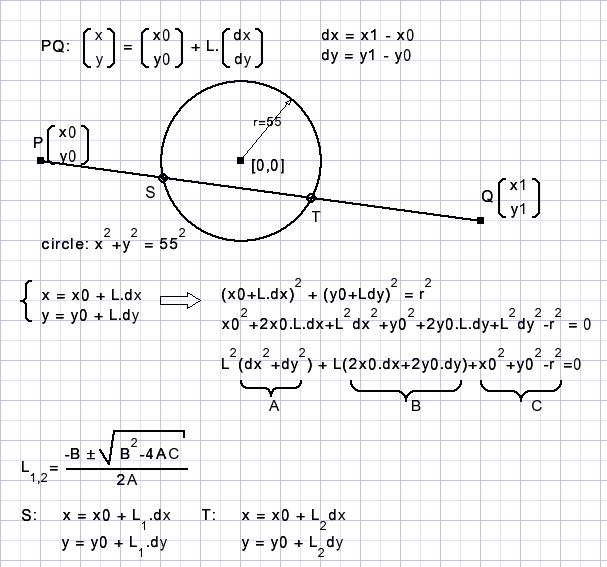
Het resultaat van berekening is lijn ST.
Tijdens verschuiven heeft het vergrootglas (midden) de co÷rdianten [magX,magY]
dat is t.o.v. de linkerbovenhoek van de bitmap.
Voor berekening:
Xoffset = (magX-500)*m Yoffset =(magY-500)*m Co÷rdinaten bijstelling voor hoekpunt [i]): X0 = m*Alist[i].rx - Xoffset Y0 = m*Alist[i].ry - YoffsetNu ligt oorsprong [0,0] precies in het midden van het vergrootglas.
Daarna volgt voor alle diagonalen een test voor snijpunten met de rand van het vergrootglas.
Geen snijpunt betekent een negatieve wortel in de formules hiervoor.
Zie procedure paintmagnifierglass; voor details.
Onthoud dat floating point waardes rx,ry in Alist[ ] relatief zijn t.o.v. het midden.
Er blijft natuurlijk nog veel te onderzoeken. Bijvoorbeeld waarom door een punt 3,4,of meer diagonalen gaan.
Het moet met symmetrie te maken hebben. Dat bewaar ik echter voor een later tijdstip.
Klik op het vergrootglas, dat plaatst het in het centrum.
Plaats de muiswijzer op het vergrootglas, beweeg de muis met de linker muisknop ingedrukt.
Dat verplaatst het vergrootglas over het scherm.
Een muisklik op het vergrootglas verwijdert het weer.
Als het vergrootglas niet geselecteerd is kunnen lijnen worden getekend.
Selecteer vooraf de kleur en dikte van de pen.
Zo kunnen regelmatige veelhoeken gebruikt worden bij de oplossing van meetkundige problemen.
Floating point berekeningen
Floating point (drijvende komma) waarden die een macht zijn van 2 (zoals 0,5 of 0,25) zijn exact.Andere waarden zoals 0,1 of π zijn benaderingen.
Berekeningen met floating point getallen zijn nooit helemaal precies.
In dit project gebruik ik 32 bit "single" floating point variabelen.
De nauwkeurigheid daarvan is 6 Ó 7 (decimale) cijfers.
Voorbeeld:
Var a,b : single; Begin .... If a = b then ....//deze conditie is meestal niet "true" // gebruik dit voor de vergelijking van kommagetallen If abs(a-b) < 1e-6 then ....// a is vrijwel gelijk aan bDe programmeur moet zich steeds realiseren hoe nauwkeurig de gebruikte variabelen zijn.

