download programma Stambreuken Elias C. Buissant des Amorie David Dirkse In dit artikel wordt beschreven hoe je een breuk kunt schrijven als som van stambreuken. Een stambreuk is een breuk, die als teller 1 heeft. Er is ook een (Windows) programma toegevoegd, dat de omzetting doet. Klik op het download (bliksem) icoontje bovenaan deze pagina om het programma te downloaden. Er is geen installatieprocedure. Kopieer het programma simpelweg naar een map. In het oude Egypte kende men geen breuken zoals bij ons. De Egyptenaren gebruikten voornamelijk stambreuken. Dat zijn breuken met 1 als teller. Er waren een paar uitzonderingen: men werkte wel met waarvoor men ook speciale symbolen had. Deze wetenschap hebben wij vooral uit de papyrus Rhind (genoemd naar mr.A.H.Rhind, die deze papyrus kocht en later aan het Brits Museum vermaakte). Deze papyrus bevat veel informatie over de stand van de wiskundekennis bij de Egyptenaren. Zo werd aangeduid als "de twee delen" De aanvulling tot 1 is dan “het derde deel”. En misschien komt daar onze benaming voor “een derde” wel vandaan. Bij deze zienswijze is het enigszins begrijpelijk dat men niet kon spreken van “drie vijfde”, want er is dan maar één vijfde deel. Opvallend is het dat de Egyptenaren breuken met teller 2 niet opsplitsten in de som van 2 gelijke stambreuken, maar schreven: De techniek van het rekenen met breuken was behoorlijk ver ontwikkeld. Elke onvereenvoudigbare breuk is te schrijven als de som van verschillende stambreuken, b.v. Maar die schrijfwijze is niet eenduidig zoals b.v. blijkt uit: Als we echter afspreken dat we steeds een zo groot mogelijke stambreuk afsplitsen, dan is de splitsing wel eenduidig. Aan de hand van een voorbeeld tonen wij aan hoe dat te realiseren is. We gaan uit van Omdat geldt : Daardoor is de grootste stambreuk die kleiner is dan Verminder met Dat levert Omdat 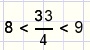geldt 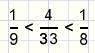Daardoor is de grootste stambreuk die kleiner is dan Verminder met Dat levert Daarmee hebben we dus gevonden Je ziet dat je steeds hetzelfde principe toepast. Maar dat totale proces kan wel heel lang duren. En het kan leiden tot stambreuken met een erg grote noemer. Probeer maar eens Als laatste noemer vonden wij 230409900. In het programma kunnen stambreuken worden verwerkt met maximaal 19 cijfers in de noemer. Daarboven wordt de mededeling gegeven: "denominator overflow". Breuken die een overflow geven zijn o.a. De langste stambreuk splitsing levert de breuk Benieuwd naar het programma? [HIER ] staat het hele Delphi-7 project.