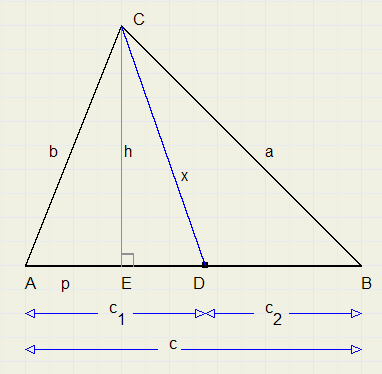
de Stelling van Stewart De Stelling van Stewart is een mooie toepassing van de stelling van Pythagoras. Zie de figuur hieronder Een driehoek heeft zijden a,b en c. Een punt D op AB verdeelt AB in stukken van c1 en c2. AE = p, CD = x We berekenen een formule voor x als a, b, c, c1 en c2 bekend zijn. Pythagoras in DEDC h2 = x2 - (c1 - p)2.........1) Pythagoras in DAEC h2 = b2 - p2...................2) ...1) en ...2) combineren: x2 - c12 + 2.c1.p - p2 = b2 - p2 x2 = b2 + c12 - 2.c1.p......................3) Pythagoras in DEBC h2 = a2 - (c - p)2.................4) ...2) en ...4) combineren: a2 - c2 +2c.p - p2 = b2 - p2 a2 = b2 + c2 - 2c.p...............5) Nu ...3) en ...5) combineren x2 = b2 + c12 - 2.c1.p ........................x c a2 = b2 + c2 - 2c.p.............................x c1 c.x2 = c.b2 + c.c12 - 2.c.c1.p.........................6) c1.a2 = c1.b2 + c1.c2 - 2c1c.p........................7) .........6) - .......7) levert: c.x2 - c1.a2 = c.b2 + c.c12 - c1.b2 - c1.c2 c.x2 - c1.a2 = b2(c - c1) - c.c1(c - c1) c.x2 = c1.a2 + c2b2 - c.c1.c2 Dit is de stelling van Stewart. De stelling is bijvoorbeeld handig bij de berekening van de lengte van een deellijn of een zwaartelijn in een driehoek. Als x zwaartelijn is dan geldt: x2 = 1/2 a2 + 1/2 b2 - 1/4 c2 En als x deellijn is dan x2 = ab - c1.c2 Het bewijs laat ik aan de lezer over.