Voorbeelden van Linaire Functies

Voorbeelden van Lineaire Functies

Onderwerpen

ññ

Evenwicht
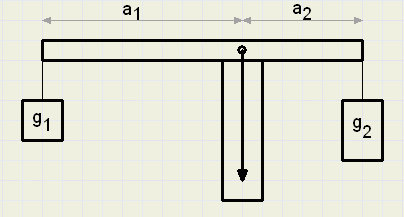
Hieronder zie je een balans afgebeeld.
Die is in evenwicht (armen in horizontale stand) als geldt:

₁

₂

waarbij g₁ het gewicht aan de linkerarm is en g₂ het gewicht
aan de rechterarm.
a₁ en a₂ zijn de lengtes van de armen.

Het product g*a heet het koppel.
Een balans is in evenwicht als de som van alle koppels aan de linkerkant gelijk is aan de som
van de koppels aan de rechterkant.
Maar je kunt ook zeggen: een balans is in evenwicht als de som van alle koppels nul is.
Dan moeten bijvoorbeeld de koppels aan de linkerkant negatief worden gerekend.

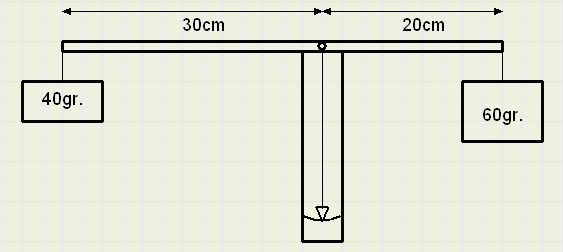De balans hierboven is in evenwicht want

40 * 30 = 60 * 20 Bekijk nu de balans hieronder.
vraag

waar moet een gewicht van 150 (gram) worden opgehangen om evenwicht te maken?

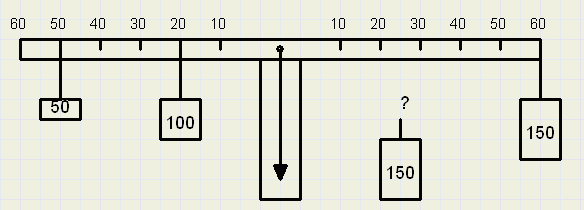We hangen de 150 gram op armlengte x , aan de rechterkant en stellen de vergelijking op:
(som van de koppels rechts = som van de koppels links)

het gewicht van 150 gram moet dus 30cm. links van het draaipunt worden opgehangen voor evenwicht.

Mengen
We gaan water mengen van verschillende temperaturen en de temperatuur
van het mengsel berekenen.
Ook berekenen we de temperatuur nadat een gloeiend stuk metaal is ondergedompeld.

De aanpak is als volgt:
warmte drukken we uit in caloriën.
Eén calorie is de hoeveelheid warmte die 1 gram water 1 graad Celsius in temperatuur doet stijgen.
Voor elke graad stijging van 100 gram water is dus nodig 100 caloriën.

Ontdooien of koken kost meer caloriën dan verwarmen van vloeibaar water.
Met die (fase) overgangen houden we ons hier niet bezig, het water blijft vloeibaar.

Samenvattend:

om g gram water T graden in temperatuur te laten stijgen zijn nodig C = g.T caloriën. Bij de volgende berekeningen bedoelen we met :
23 gram water van 20 graden bevat 20 * 23 = 460 caloriën"
dat er bij een temperatuur van 0 graden 460 caloriën zijn toegevoegd om
een temperatuur van 20 graden te bereiken.

Berekening
Stel nu, dat we 120 gram water hebben van 60 graden en 75 gram water van 15 graden.

Welke temperatuur zal het water hebben na menging?

Er gaan geen caloriën verloren, stel de temperatuur na menging t , dan

Soortelijke Warmte
De soortelijke warmte S van een stof is

S =

c a l

g r a m.g r C e l s i u s

Oftewel:
S is het aantal caloriën dat nodig is om 1 gram van de stof 1 graad celsius in temperatuur te laten stijgen.
Voor water is de soortelijke warmte gelijk aan 1.

Voorbeeld
Aan 75 gram van een stof worden 300 caloriën warmte toegevoegd.
Daardoor stijgt de temperatuur 18 graden.
De soortelijke warmte C is dan:

C =

300

18 · 75

= 0.222

Hieronder zie je een tabelletje staan met de soortelijke warmte van enkele stoffen

aluminium	0,215
goud	0,03
ijzer	0,1
tin	0,05
zink	0,09

Samenvattend:

Berekening 1.
200 gram ijzer van 200 ⁰Celsius dompelen we onder in 350 gram water van 25 ⁰Celsius.
Voor de eindtemperatuur t stellen we de vergelijking op :

⁰

Berekening 2.
In een goed geïsoleerd aluminium vat van 320 gram wordt 150 gram water van 70 graden gegoten.
De temperatuur van het lege vat is 18 graden.
Het water zal warmte afstaan aan het vat.
Stel T is de temperatuur van het gevulde vat, dan

Communicerende vaten
Hieronder is afgebeeld een drietal cilindrische vaten, die met leidingen zijn verbonden.
Het linker vat is geheel gevuld met water.
De andere vaten zijn leeg en de kranen in de leidingen zijn dichtgedraaid.
Als de kranen worden geopend zal water van het linker- naar de andere vaten stromen
zolang het niveau van het water in de vaten ongelijk is.
Na enige tijd is het waterniveau in alle vaten gelijk.
Dat heet de "wet van de communicerende vaten".

Opmerking: de hoeveelheid vloeistof in de leidingen tellen we in het vervolg niet mee.

vraag:

- wat zal de uiteindelijke hoogte (h) zijn van het water?

Stel, dat de hoogte van het water in de vaten h meter is.
Dan is de hoogte in het middelste vat (h - 1) en in het rechter vat (h - 2) meter.

Opmerking: de inhoud I van een cilindrisch vat met hoogte h en diameter d bedraagt

.....{opp. grondvlak x hoogte}

Voor en na het openen van de kranen is de hoeveelheid water gelijk,
zodat we de vergelijking opstellen

.....{delen door 0,25*p}

.....{kwadraten weg}

.....{haakjes weg}

.....{alle termen met h samenvoegen}

.....{termen zonder h naar links en samenvoegen}

.....{omdraaien}

.....{delen door 7,69}

Verdelen
Drie schurken A,B en C verdelen de buit van een overval ( €82000) als volgt:

Hoeveel ontvangt elk?

Stel A ontvangt a euro's.
dan ontvangt B dus a + 22000 en
C ontvangt 0,60(a + 22000)

zodat we de vergelijking kunnen opstellen:

A ontvangt 18000, B 18000 + 22000 = 40.000 en C ontvangt 0,6*40.000 = 24.000

Gemiddelden
Het gemiddelde G_n van n bedragen B₁, B₂ .... B_n is

G_n =

B₁ + B₂ + ... + B_n

Voorbeeld
Het gemiddelde van de getallen 82, 122, 206 en 76 is

G = (82 + 122 + 206 + 76) / 4 = 121,5 Berekening
Een rapportcijfer is het gemiddelde van de cijfers van 4 proefwerken.
Een leerling heeft als rapportcijfer een 7 en de proefwerkcijfers zijn 5, 9 en 6.
Het vierde proefwerkcijfer (x) is niet bekend, maar kan als volgt worden berekend:

7 =

5 + 9 + 6 + x

Weegfactoren
Het gemiddelde G_n van n gewogen bedragen B₁....B_n met weegfactor w_i voor B_i is

G_n =

w₁ B₁ + w₂ B₂ + ... + w_n B_n

w₁ + w₂ + ... + w_n

Voorbeeld
Een leerling heeft behaald

Het eindcijfer zal zijn

G_n =

3 · 6 + 3 · 7 + 8 + 3 + 5 + 2 · 9

3 + 3 + 1 + 1 + 1 + 2

Berekening 1.
Klas H3A bestaat uit 12 leerlingen. het gemiddelde voor het vak Duits is 6,3.
Klas H3B staat gemiddeld 5,4 voor Duits.
Klassen H3A en H3B worden samengevoegd en het gemiddelde voor het vak Duits van
geheel H3 is dan 5,77.
Vraag:

bereken het aantal leerlingen in klas H3b

Bedenk, dat het aantal leerlingen de weegfactor is bij berekening van het gemiddelde.
Stel dat H3B n leerlingen telt, dan geldt:

5 , 77 =

12 · 6.3 + n · 5.4

12 + n

H3B telde dus 17 leerlingen.

Berekening 2.
In steden A (120.000 stemgerechtigde inwoners) en B (45.000 stemmers) wordt een stemming gehouden.
In A stemt 50% voor, terwijl de inwoners van A en B samen 55% voor stemmen.

welk percentage van B stemde voor?

De aantallen stemgerechtigden zijn de weegfactoren.
Stel, dat in B een percentage p voor stemde, dan

0.55 =

0.5 · 120000 + p · 45000

120000 + 45000

68,3 procent van de stemmers in B stemde dus voor.

Achtervolgen
Persoon A vertrekt op tijdstip 0 vanuit dorpje P .
A beweegt zich voort met constante snelheid v_A{v is afkorting van "velocity"}

Persoon B vertrekt d uren {d is afkorting van "delay"} later uit P en achtervolgt A.
B beweegt zich voort met constante snelheid v_B.

De volgende vragen komen op:

- na hoeveel tijd heeft B A ingehaald?
- na hoeveel kilometer is dat?

Na t uren heeft A afgelegd een afstand {afstand = snelheid * tijd}

Als A t uren onderweg is, dan is B dus (t - d) uren onderweg omdat B d uren later is vertrokken.
B heeft dan afgelegd:

Op het moment van ontmoeting zijn de afgelegde afstanden gelijk, zodat

...............{haakjes wegwerken}

...............{termen met t naar links}

............{t buiten haakjes halen}

............{delen door v_A - v_B}

............{vermenigvuldigen met -1}

............{- teken wegwerken}

t =

v_B d

v_B − v_A

..........[1]

Om de afgelegde afstand S te vinden wordt de waarde van t gesubstitueerd in S_A = v_At.

S =

v_A v_B

v_B − v_A

..........[2]

Getallenvoorbeeld
A fietst met een snelheid van 18km per uur.
B begint de achtervolging 2,5 uur later en beweegt zich per bromfiets voort met 33 km. per uur.
Gebruik formule [1] om t te berekenen, de tijd dat de achtervolging duurt:

t =

33 − 18

· 2 , 5

De afgelegde afstand is dan

Dezelfde afstand wordt natuurlijk ook gevonden met

Variatie 1
We vragen ons af, wat op elk moment de afstand tussen A en B is.
Dat is niet met een formule te beschrijven als we beginnen te meten bij het vertrek van A.
Immers, B staat dan nog enige tijd stil om plotseling een snelheid v_B te krijgen.
Zo'n beweging levert een grafiek op met een knik, wat niet kan, er is geen formule
die zo'n beweging beschrijft.
Daarom gaan we de tijd rekenen vanaf het vertrek van de achtervolger B.
We laten A e uur eerder vertrekken.
Als B t uren onderweg is, dan is A dus (t + e) uren onderweg.
Hun onderlinge afstand S_AB = S_A - S_B wordt dan:

_AB

Deze laatste formule staat wat aardiger en geeft ook minder rekenwerk.

Variatie 2
Stel, dat we de snelheid van de achtervolger willen berekenen als bekend is in welke tijd
A wordt ingehaald.
We gaan uit van formule [1]

t =

v_B

v_B − v_A

....{vermenigvuldigen met (v_B - v_A)}

zodat

....{haakjes weg}

....{termen met v_B naar links}

....{v_B buiten haakjes halen}

....{delen door (t - d)}

v_B = v_A ·

t − d

.......[3]

Getallenvoorbeeld
Stel dat B 1,2 uur na A vertrekt.
A heeft een snelheid van 72 km per uur en wordt ingehaald 4,6 uur na zijn vertrek.
De snelheid van de achtervolger was dan volgens [3]

v_B =

72 · 4.6

4.6 − 1.2

= 97.41

opmerking: Lees een komma voor de decimale punt in de formule hierboven.

Opgaven (en antwoorden)
[1]
Zie figuur hieronder.

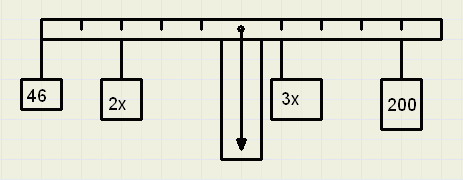Links en rechts bevinden zich onbekende gewichten, die zich verhouden als 2 : 3.
(Noem ze dus 2x en 3x).

bereken de onbekende gewichten.

[2]
Een geïsoleerde aluminium pan weegt leeg 400 gram.
De pan bevat 700 ml. water van 23 ⁰C.
Aan de pan wordt toegevoegd

⁰

Opmerking: het metaal van de pan neemt ook warmte op.

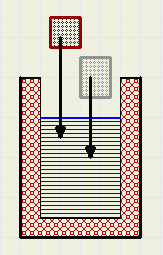bereken temperatuur daarna.

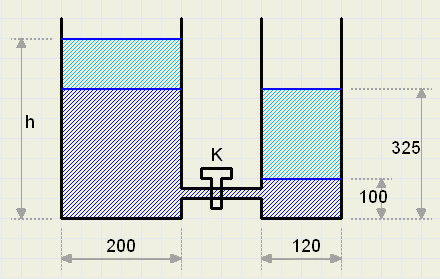
[3]
Hieronder zie je twee communicerende vaten.
De waterhoogte in het linker vat is onbekend, in het rechtervat staat het water 100cm. hoog.
Na openen van de kraan K stabiliseert de waterhoogte in beide vaten zich op 325cm.
De vaten zijn cilindrisch, doorsnede is aangegeven in cm.

bereken oorspronkelijke waterhoogte h van het linkervat.

[4]
Vier familieleden , A, B, C en D verdelen een erfenis van €160.000
De overledene heeft het volgende bepaald:

hoeveel erft elk familielid?

[5]
Twee groepen A en B, maken een examen.
In groep A wordt gemiddeld het cijfer 6,0 gescoord en in groep B
is het gemiddelde cijfer 7,2.
De groepen worden samengevoegd waardoor het gemiddelde cijfer per deelnemer 6,8 wordt
. Groep A telde 20 deelnemers.

bereken het aantal deelnemers van groep B.

[6]
A fietst met een constante snelheid van 21,9 km/uur.
B vertrekt 3 uur na A en achtervolgt A met constante snelheid.
Zodoende wordt A na 8,1 uur ingehaald.

bereken de gemiddelde snelheid van B.

Antwoorden:

[1]: x = 190
[2]: t = 33,06 graden Celsius
[3]: h = 441,64 cm
[4]: A 25000 B 40000 C 60000 D 35000
[5]: 40
[6]: 30 km/uur