Constructie van een Regelmatige Vijfhoek

Inleiding
Dit artikel beschrijft de constructie met passer en liniaal van een regelmatige vijfhoek.
Daarna wordt uitgelegd waarom deze constructie correct is.

De Constructie
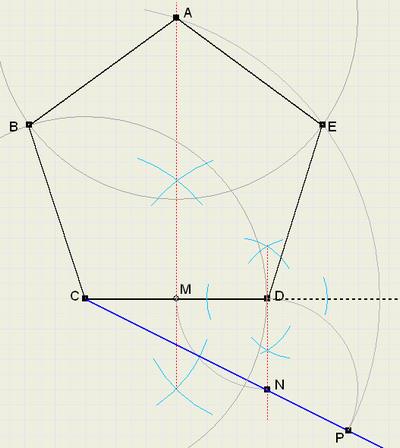
Bekijk figuur 1.
ABCDE is hier de geconstrueerde vijfhoek.

    fig. 1

De constructie bestaat uit de volgende stappen:
    1. kies de lengte van lijnstuk CD, de basis van de vijfhoek
    2. construeer het midden M van CD
    3. richt loodlijn op vanuit D
    4. pas DM af op loodlijn, DN = DM
    5. verleng lijnstuk CN
    6. cirkel DN om vanuit N, pas af op verlengde CN, CP = CN + DN
    7. verleng middelloodlijn van CD
    8. cirkel CP om vanuit C, A is snijpunt met middelloodlijn van CD
    9. cirkel CD om vanuit middelpunten A, C en D. Dat levert punten B en E

Waarom klopt dit?
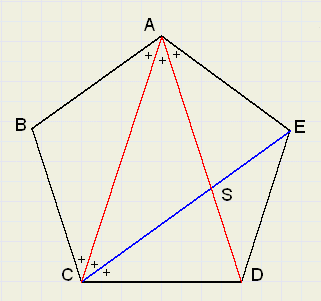
Bekijk figuur 2.
    fig. 2

Een hoekpunt van de vijfhoek is 108 graden.
Dat is als volgt te zien:
    Verdeel de vijfhoek vanuit het midden in 5 driehoeken
    Het totaal van alle hoeken is dan 5 * 180 = 900 graden.
    Trek hier de middelpunten vanaf, 900 - 360 = 540 graden.
    Elk hoekpunt is 540 / 5 = 108 graden.
Driehoek CDE is gelijkbenig, zodat
LECD = LCED zodat


Elke met + gemerkte hoek is 36 graden.

CS is de deellijn van LACD

LCSD = LSDC = 72 graden, zodat
    CD = CS = SA
Stel de lengte van CD = 1.

Vierhoek ABCS is een ruit, zodat AS = BC = 1

We passen de stelling toe, dat in een driehoek de deellijn van een hoek de overstaande zijde
verdeelt in lijnstukken die zich verhouden als de aanliggende zijden.
Oftewel:
    AC : CD = AS : SD
Als we stellen AC = x dan geldt :
    x : 1 = 1 : ( x - 1 ) .................of
    x2 - x - 1 = 0
de ABC formule levert:
x =
Als we kunnen aantonen, dat CP = x dan is het bewijs geleverd.

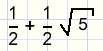Die berekening wordt aan de lezer overgelaten.