de Volgcurve of Achtervolgingskromme

In figuur 1. hieronder is getekend een zg. "volgcurve" of ook wel genoemd "achtervolgingskromme".
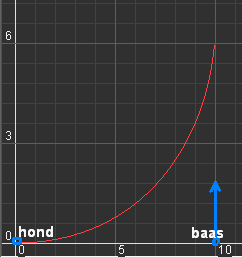    fig.1
Op tijdstip 0 staat een hond in (0,0) en zijn baas in (10,0).
De baas loopt met constante snelheid naar boven evenwijdig aan de y-as.
De hond loopt, eveneens met constante snelheid, steeds recht op zijn baas af.
De baan (curve) van de hond is rood getekend.
De verhouding "snelheid hond : snelheid baas" is hier 2 : 1

Gevraagd wordt de vergelijking van deze volgcurve, die de vorm heeft: ...y = ... x ....

Merk op :
d y
d x
 ... is dus de richting (richtingscoëfficiënt) waarin de hond loopt.

Laat op tijdstip 0 de hond vertrekken uit punt (0,0) en de baas uit (a,0).
Na enige tijd heeft de baas een afstand b gelopen en bevindt zich in punt (a,b).
De hond is dan aangekomen in punt H(x,y).
Zie figuur 2.
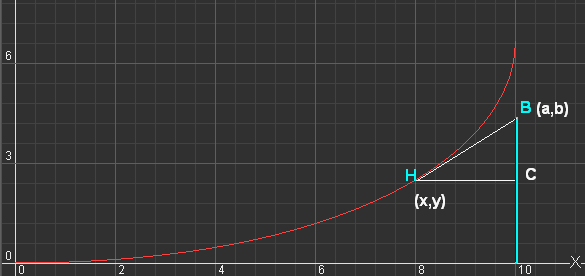    fig.2
Uit de figuur volgt:
    d y
    d x
     = 
    B C
    H C
     = 
    b − y
    a − x
zodat:
    b = y + (a − x) · 
    d y
    d x
en
    d b
    d x
     = 
    d y
    d x
     + (a − x) · 
    d 2 y
    d x 2
     − 
    d y
    d x
    d b
    d x
     = (a − x) · 
    d 2 y
    d x 2
Laat s de afgelegde weg van de hond zijn.
Omdat de baas v * sneller loopt dan zijn hond geldt:.......
    ds = v-1db
zodat
    d s
    d x
     = v −1 (a − x) · 
    d 2 y
    d x 2
    d s = v −1 (a − x) · 
    d 2 y
    d x 2
     d x     ...........................[1]
We beschouwen het stukje ds van de curve, die de hond vanuit H aflegt.
Er geldt:
    (ds)2 = (dx)2 + (dy)2
    (d s) 2 = (d x) 2 
    æ1 + 
    2
    æ
    d y
    d x
    		ö
    ­­
    èø
    		ö
    ­­
    èø
    d s = 
    \1 + 
    2
    æ
    d y
    d x
    		ö
    ­­
    èø
    		 d
    		 x
     ...........................[2]
Combinerend [1] & [2]:
    \1 + 
    2
    æ
    d y
    d x
    		ö
    ­­
    èø
    		 d
    		 x
    		 = v −1 (a − x) · 
    d 2 y
    d x 2
     d x
Stel
d y
d x
 = p , zodat
    \1 + p 2
     = v −1 (a − x) · 
    d p
    d x
    d p
    \1 + p 2
    		 = 
    v. d x
    a − x
Deze differentiaalvergelijking heeft als oplossing:
    ln
    æp + 
    \1 + p 2
    		ö
    èø
     = −v ·  ln (a − x) +  ln c
    p + 
    \1 + p 2
     = c (a − x) −v     ...........................[3]
Voor de oplossing van p is het handig eerst het wortelgedeelte te elimineren.
Dat kan als volgt, als we bedenken dat
    1
    p + 
    \1 + p 2
    		 = 
    p − 
    \1 + p 2
    p 2 − (1 + p 2)
    		 = −p + 
    \1 + p 2
dus
    −p + 
    \1 + p 2
     = c −1 (a − x) v     ...........................[4]
Aftrekken ...[3] - [4]:
    2 p = c (a − x) −v − c −1 (a − x) v
Uit de randvoorwaarden is c te berekenen.
Op t = 0 geldt p = x = y = 0 zodat:
    0 = ca-v - c-1av
    c = av
Zodat
    2 p = a v (a − x) −v − a −v (a − x) v
    2 p = 
    a v
    (a − x) v
     − 
    (a − x) v
    a v
    2 p
         		 = 
     
    1
    v
    æ1 − 
    x
    a
    		ö
    ­­
    èø
    		 − 
     
    v
    æ1 − 
    x
    a
    		ö
    ­­
    èø

     
    2 p = 
    −v
    æ1 − 
    x
    a
    		ö
    ­­
    èø
     − 
    v
    æ1 − 
    x
    a
    		ö
    ­­
    èø
Integreren
    2 y = −
    a
    1 − v
     
    1 − v
    æ1 − 
    x
    a
    		ö
    ­­
    èø
     + 
    a
    1 + v
     
    1 + v
    æ1 − 
    x
    a
    		ö
    ­­
    èø
     + C
Omdat voor x = 0 ook y = 0 vinden we :
    C = 
    2 a v
    1 − v 2

De gezochte curve heeft dus als vergelijking:
    2 y = −
    a
    1 − v
     
    1 − v
    æ1 − 
    x
    a
    		ö
    ­­
    èø
     + 
    a
    1 + v
     
    1 + v
    æ1 − 
    x
    a
    		ö
    ­­
    èø
     + 
    2 a v
    1 − v 2
De hond haalt zijn baas in als x = a, dan geldt
    y = 
    a v
    1 − v 2
     ................[5]
Hoeveel tijd t heeft de hond nodig om zijn baas in te halen?
b = vt is de afgelegde weg van de baas met snelheid v,
voor x = a geldt y = b = vt, combineer met ...[5] en
    t = 
    a
    1 − v 2
Opmerking:
zie figuur 2.
hierin is a = 10 en v = 0,5 dwz. de hond loopt 2 x zo snel als zijn baas.
Na t = 13,33 wordt de baas ingehaald.

We willen nu weten hoelang er is gelopen bij een bepaalde waarde van x.
Aangezien de hond snelheid 1 heeft, is deze tijd gelijk aan de lengte van de curve die de hond
van 0 tot x heeft afgelegd.

De lengte van de curve is
    ó
    õ
    \1 + p 2
     dx
We gaan uit van het eerder verkregen resultaat
    2 p = 
    −v
    æ1 − 
    x
    a
    		ö
    ­­
    èø
     − 
    v
    æ1 − 
    x
    a
    		ö
    ­­
    èø
om schrijfwerk te besparen stellen we
    u = 1 − 
    x
    a
     ..............zodat
    p = 
    1
    2
     (u −v − u v)
    p 2 = 
    1
    4
     (u −2 v + u 2 v − 2)
    1 + p 2 = 
    1
    4
     (u −2 v + u 2 v + 2)
    1 + p 2 = 
    1
    4
     (u −v + u v) 2
    \1 + p 2
     = 
    1
    2
     (u −v + u v)
de booglengte S = 
1
2
 
ó
õ		(u −v + u v) dx
 ......[6]
en omdat dx = -a du gaat ...[6] gaat over in
    S = 
    -a
    2
     
    ó
    õ    		(u −v + u v) du
Integreren:
    S = 
    −a
    2
     
    æ
    u 1 − v
    1 − v
     + 
    u 1 + v
    1 + v
    		ö
    ­­
    èø
     + C
u vervangen:
    S = 
    −a
    2 (1 − v)
     
    1 − v
    æ1 − 
    x
    a
    		ö
    ­­
    èø
     − 
    a
    2 (1 + v)
     
    1 + v
    æ1 − 
    x
    a
    		ö
    ­­
    èø
     + C
Voor x = 0 is S = 0, zodat
    S = 
    −a
    2 (1 − v)
     
    1 − v
    æ1 − 
    x
    a
    		ö
    ­­
    èø
     − 
    a
    2 (1 + v)
     
    1 + v
    æ1 − 
    x
    a
    		ö
    ­­
    èø
     + 
    a
    1 − v 2
S is de afgelegde booglengte van 0 tot x. Deze is ook gelijk aan de tijd,
omdat de hond de (relatieve) snelheid 1 heeft.

Vraag
De positie van de hond in het coördinatenstelsel H(x,y) zou ook aangegeven kunnen worden
met x en y afhankelijk van de tijd t, dus in parametervorm x(t) ; y(t).

Het lukt mij echter niet deze parametervoorstelling uit het bovenstaande af te leiden.
Wie helpt?

Naar aanleiding van bovenstaande vraag ontving ik een uitgebreid antwoord van de heer F. Antheunus (België).

Hieronder staan zijn drie (.doc) bestanden in .zip formaat: