How to calculate with fractions

When counting events or people we deal with whole numbers....0,1,2,3,...also called integers.
However in the case of measuring gallons, temperatures or the length of an object,
any value between whole numbers may result.
Such numbers we call fractions or reals.
In this article the rules for calculations with fractions are explained.

Notation

In the picture below a chocolate bar is cut in five equal pieces.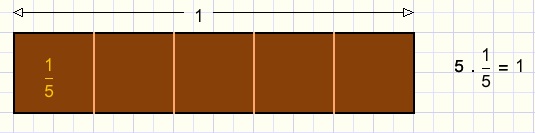

In this picture the point "." stands for multiplication.
Each piece is one fifth.
The upper number (1) is called the numerator.
The lower number (5) is called the denominator.

The numerator is the original object.
The denominator is the number of equal pieces that together make the object.

In the next picture we divide 2 chocolate bars in 5 equal pieces

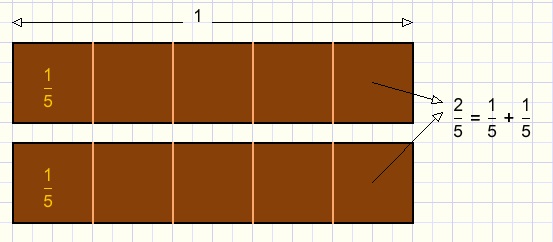
Addition

How to add fractions?
This rule directly follows from the distributive law:

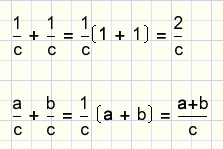
In words: if the denominators are equal, add (subtract) the numerators.

Multiplication

For this rule we use a chocolate tablet with a total surface of 1.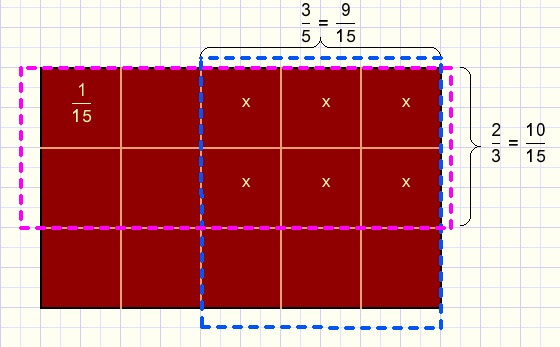

The above figure illustrates that:

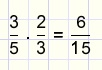
The general rule is:

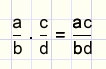
In words: numerator * numerator, denominator * denominator.
There is no need for the denominators to be equal.

for a proof we need the commutative law for multiplication: ab = ba

Equal fractions

A fraction does not change if numerator and denominator are both multiplied (divided) by the same number.
This rule directly follows from the multiplication rule:

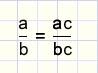
proof:

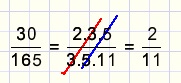
Reduction

With the above rule fractions may be reduced by dividing
both numerator and denominator by a common (prime) factor.
See example below:

Adding any fractions

This can be done by first multiplying the fractions to obtain equal denominators.

Note:
Multiplying the denominators may result in larger numbers then necessary.
The Least Common Multiple of the denominators will do.
Say L = LCM(b,d) and G = GCD(b,d) and knowing that L . G = bd then:

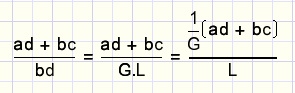
This results in the smallest possible denominator and the resulting fraction does not need reduction.

Example:

Combining integers and fractions

writing integer as fraction	notation	combining integer and fraction

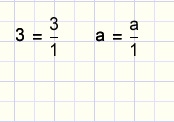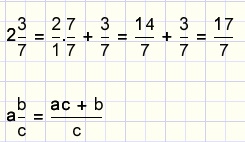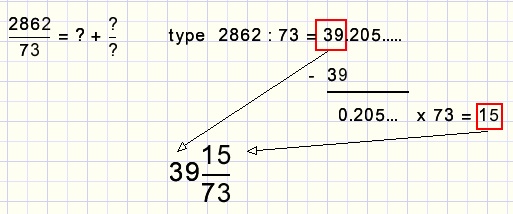
using pocket calculator to extract integer part from a fraction:

Reciprocal of a fraction

If the numerator and the denominator of a fraction change place, the result is the reciprocal fraction.
A fraction multiplied by it's reciprocal results in "1".

Division by a fraction

Division by a fraction is accomplished by multiplying by it's reciprocal value.

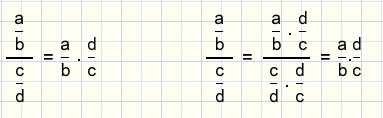
Example:

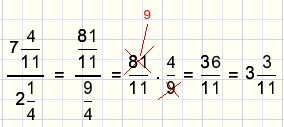
Note:
The Cray-1 supercomputer had no instruction for division.
Instead, it calculated reciprocal values and used multiplication.

Percentages

A percentage is the numerator of a fraction that has 100 as denominator.
Example of writing a fraction as percentage:

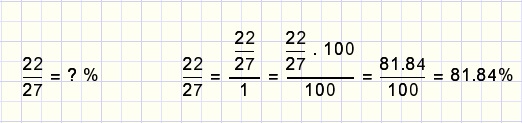
Using a pocket calculator simply type: 100 x 22 : 27 = 81.84

An application

A fraction like 3/5 may be regarded as

Both cases have the same result.

1. Distribution
A sum of $12000 has to be distributed over three people A,B,C such that A:B:C = 2:3:5.
How much does anyone receive?

2+3+5 = 10.
A recieves: (2/10)*12000 = 2400
B receives: (3/10)*12000 = 3600
C receives: (5/10)*12000 = 6000

2.Probability
When throwing a dice there are 6 possible outcomes: 1..6.
The chance for 6 is 1/6.
When throwing 2 dice there are 6*6=36 possible outcomes: (1,1)..(6,6).
The chance for (6,6) is 1/36.
When we throw 2 dice hundred times we expect (1/36)*100 = 2....3 times a (6,6) outcome.

3.Water flow
Picture below shows a pipeline system for water.

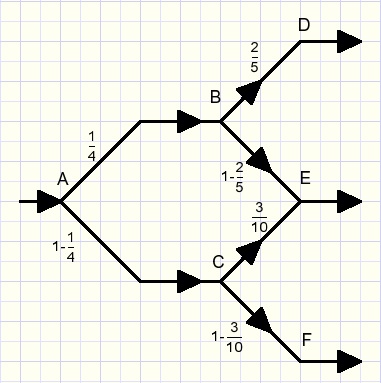
At A the flow divides: 1/4th flows to B, so 1-(1/4)=3/4 flows to C.
Flow A-B-D: 1/4 . 2/5 = 1/10
Flow A-C-F: 3/4 . 7/10 = 21/40
Flow A-B-E: 1/4 . 3/5 = 3/20
Flow A-C-E: 3/4 . 3/10 = 9/40
Flow out of E: 3/20 + 9/40 = 15/40 = 3/8
check: adding flows out of D,E,F: 1/10 + 3/8 + 21/40 = 1

For every thousand gallons of water flowing in at point A,
(3/8) * 1000 = 375 gallons flow out at point E.

Note:
serial flow: multiply fractions.
parallel : add fractions.