LCM and GCD

Introduction
This article is about LCM (least common multiples) and GCD (greatest common divisors),
which belongs to the basics of number theory.
This involves also factorization and prime numbers.
The prerequisite is grammar school.

the Natural numbers
These are the numbers 0,1,2,3,4,5,.................etcetera.
There are an infinite number of natural numbers.
    Counting blocks involves natural numbers

This articles is about natural numbers, no fractions, no real- or complex numbers.

Factors
A number which multiplies another number we call a factor.
The multiplication 6 * 2 * 4 * 11 shows 4 factors:
the first is 6, the second is 2 ...etcetera.
A factor denotes the amount of something.

Dimension
In geometry dimension is length, height or width.
In fysics dimension is the type of measurement unity.
Degrees Celsius is the dimension of temperature, meters per second is the dimension of speed.

The property length may have meter as dimension.
If a bar of 2 meters is multiplied by a factor 3 we obtain a bar of 6 meters length.
The property length has changed but it is still a bar.

Factors have no dimension.
If we multiply something (weight, time,distance) by a factor the dimension does not change.

However, if we multiply numbers that both have a dimension we obtain something new.
meter * meter = square meter; electricity: current * voltage = power.

The amouny of labour to program a computer game is measured in man hours. ManHours being a new dimension.

This article assumes dimension free numbers.
All numbers are factors.

Terms
Numbers that are added are called terms
12 + 9 + 23 is an addition of 3 terms.
it is only possible to add terms that have the same dimension.
If a and b are unknown phenomena, the addition a + b is not possible.
If a is a factor 3 and b is a factor 5 and the dimension is "chicken"
we may calculate a + b = 3 + 5 = 8 {chickens}.

Multiples
The multiples of 5 are :
    5, 10, 15, 20, 25,...........
In general:
    the multiples of 5 we may write as 5*k , where k = 1,2,3,4,5,6,........

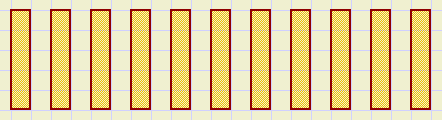    multiples of 5
Example:
the multiples of 11 are: 11, 22, 33, 44, 55, 66, 77, .......

If we have a pile of stones and the amount is a multiple of 5 then we may sort
the stones in groups of 5 and no stone is left.

Divisors
If the stones are sorted in groups of 5 we can count the number of groups.
This is called division by 5.
Or: if 5 persons honestly distribute the stones, everybody recieves a stone from each group
and no stone is left.
But such a distribution is possible only if the number of stones is a multiple of 5 or:
may be written in the form 5.k.

So, these statements are similar:
(if one is true, the others are also true)
    - 35 can be divided by 5
    - 35 is a multiple of 5
    - 35 has a factor 5
    - the division 35 / 5 has zero as remainder
    - 35 may be written in the form 5.k

Prime numbers
Primes (prime numbers) are natural numbers that have no factors. (other than itself).

The first 10 prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29

Any natural number may be written as a factorization of prime numbers.
The -prime- factors are unique for each number.

Factorization
just look:
    100 = 2 * 50
    50 = 2 * 25
    25 = 5 * 5
so:
    100 = 2 * 2 * 5 * 5 = 22 * 52
Writing 100 as 22 * 52 we call: factorization.
Prime numbers may be regarded as the building blocks of natural numbers.

Each number may be factorized in one unique way only.
Natural numbers are equal if they contain the same factors.

In the notation 52 we call 5 the base and 2 the exponent.
The exponent denotes the amount of factors of the base.

Numbers 2 and 5 cannot be factorized:
an amount of 2 or 5 stones cannot be split in equal groups.

the Sieve of Eratosthenes
Eratosthenes was a Greek mathematician who lived 276 - 194 BC.

His "sieve" is a method to find prime factors in a number.
To find the prime factors in the number 100, we write down all natural numbers 2...100 in a table.
Now proceed as follows:
    1. Mark the first prime number, which is 2.
    2. Cross out all multiples of 2 (4,6,8...) because multiples cannot be prime.
    3. proceed to the next uncrossed number which is 3, the next prime factor.
    4. Cross out all multiples (6,9,12,15,...) .
    5. repeat steps 3,4.
Below you see a table in which the sieve is applied.
Multiples are colored differently.
                   2   3   4   5   6   7   8   9
          10  11  12  13  14  15  16  17  18  19
          20  21  22  23  24  25  26  27  28  29 
          30  31  32  33  34  35  36  37  38  39
          40  41  42  43  44  45  46  47  48  49
          50  51  52  53  54  55  56  57  58  59
          60  61  62  63  64  65  66  67  68  69
          70  71  72  73  74  75  76  77  78  79
          80  81  82  83  84  85  86  87  88  89
          90  91  92  93  94  95  96  97  98  99
The multiples of 2 are colored purple.
The first purple number is 4.
The multiples of 3 are colored green-blue.
The first number of this color is 9.
From here we may draw an important conclusion:
if we have crossed out all multiples of prime number p we know for sure
dat all uncrossed numbers until p*p are prime.
To find all prime numbers up to 1000 we only need to cross out multiples of 2..31

Systematical factorization
In this example we factorize the number 4126200 and use a pocket calculator.

A simple but lengthy method:
    - transfer 4126200 to the memory of your calculator
    - divide by , the first prime, quotient is 2063100
    - write down factor 2 and save 2063100 in memory
    - again divide by 2, quotient is 1031552
    - write down factor 2, save 1031552 in memory
    - again divide by 2, quotient is 515775
    - write down 2, save 515775 in memory
    - again divide by 2, quotient is 257887.5 (number has no factor 2)
    - reload 515775
    - divide by 3, quotient is 171925
    - write down factor 3, save quotient in memory
    - again divide by 3, quotient is 57308,33333 (no factor 3 )
    - reload 171925
    - divide 171925 by 4
    (impossible to find a factor 4, because 4 = 2 * 2)
    - divide 171925 by 5, quotient is 34385
    - write down 5, save quotient in memory
    - again divide by 5, quotient is 6877
    - write down 5, save quotient
    - again divide by 5, quotient is 1375.4
    - reload 6877
    - divide by 6,7,8,9,10,11,12....as long as quotient is a natural number. Else reoad.
    - 6877 / 13 = 529, write down factor 13, save quotient.
    - divide 529 by 13,14,15,16,17,18,19,20,21,22.....reload if quotient is not a natural number
    - 529 / 23 = 23, wriet down factor 23, save 23.
    - 23 : 23 = 1, write down factor 23.(do not forget last factor)
The factors that were written down: 2,2,2,3,5,5,13,23,23, so:
    4126200 = 23*3*52*13*232
First improvement.
 A prime number larger than 3 has the form 6.k - 1 or 6.k + 1.
Reason: 6.k, 6.k + 2, 6.k + 3, 6.k + 4 cannot be prime because they have divisors 6, 2, 3 or 2.
We may limit our divisors to 2, 3, 5, 7, 11, 13, 17, 19, 23, 25, 29, 31, 35, 37,.....

Second improvement.
 Save the first prime numbers in a table.

Third improvement.
 Say we want to factorize the number 5113.
We try division by previously stored prime numbers.
At one moment we divide 5113 / 71 = 72,01....
and next 5113 / 73 = 70,04...
For the first time the quotient is smaller than the divisor.
Now we can stop dividing. If 5113 contained a factor we already had encoutered before.
Conclusion: 5113 prime.

Smart notation:
    quotientdivisor
    41262002
    20631002
    10315502
    5157753
    1719255
    343855
    687713
    52923
    23
The divisors together with the last quotient make the factors.

The LCM (least common multiple)
The multiples of 12 are: 12, 24, 36, 48, 60, 72, 84, 96, .....
The multiples of 15 are: 15, 30, 45, 60, 75, 90, 105, 120, ......
The least common multiple is : 60.

Because:
    60 = 5 * 12
    60 = 4 * 15
Notation:
    LCM(12,15) = 60
12 divides 60, because 60 contains all factors of 12.
15 is a divisor of 60, because 60 contains all factors of 15.

Factors that are present in both 12 and 15 (factor 3) need to be counted just once.

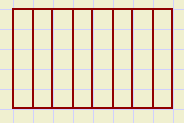
    LCM(6,10) = 30
Calculation of LCM(12,15) by factorization:
    12 = 22 * 3
    15 = 3 * 5
Compare the factors of the numbers and select the maximum per factor.
In this case: 2 factors of 2 (12) and 1 factor 3, 1 factor 5 (15).
Dus LCM(12,15) = 22 * 3 * 5 = 60.

Example:
    2520 = 23 * 32 * 5 * 7
    29700 = 22 * 33 * 52 * 11
So:
    LCM(2520,29700) = 23 * 33 * 52 * 7 * 11 = 415800

GCD (greatest common divisor)
Divisors of 120 are:
    2,3,4,5,6,8,10,12,15,20,24,30,40,60,120
Divisors of 48 are:
    2,3,4,6,8,12,16,24,48
The greatest common divisor is 24.

All factors of 24 are also present in 120 and in 48.
24 is built with the common divisors of 120 and 48.

Notation:
    GCD(120,48) = 24
Calculation of GCD(120,48) by factorization:
    120= 23 * 3 * 5
    48 = 24 * 3
Observe the factors of the numbers and select per factor the smallest amount.
This are 3 factors 2, 1 factor 3 and 0 (no) factor 5, so:
    GGD(120,48) = 23 * 3 = 24
Example:
    2520 = 23 * 32 * 5 * 7
    29700 = 22 * 33 * 52 * 11
Zodat:
    GCD(2520,29700) = 22 * 32 * 5 = 180

The relation between LCM and GCD
In the case of LCM we selected per factor the greatest exponent.
In the case of GCD we selected per factor the smallest exponent.
Selecting both we simply obtain the product of both numbers so:
    LCM(a,b) * GCD(a,b) = a * b
This is a very useful rule.

Example:
    LCM(2520,29700) * GCD(2520,29700) = 415800 * 180 = 74844000
    but also: 2520 * 29700 = 74844000

Relative primes
Numbers are called "relative prime" if they have no common factors.
An example is 16 and 25.
In case of relative primes a,b we see: GCD(a,b) = 1.

The Euclid theorem
Euclid was a Greek mathematician who lived 325 - 265 BC.
He invented a nice way to calculate the GCD of two numbers without factorization.

This is his rule: (if a > b)
    GCD(a,b) = GCD(a-b,b)
Repetitive application of this rule is the tric.

Example:
    GCD(630,300) = GCD(330,300) = GCD(300,30) = .... = GCD(30,30) = 30.
Proof of: GGD(a,b) = GGD(a - b, b)
The proof has two parts:
    1. if d is a factor of both a and b, then d also is a factor of a - b
    {no factors are lost}
    2. if d is a factor of a - b and also of b, then d also is a factor of a
    {no factor is added}
    - =
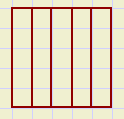    the difference of the multiples of 5 also has a factor 5

proof 1.
    assume:
    a = p.d and b = q.d, where p and q are relative prime.
    Then:
    a - b = p.d - q.d = d(p - q)
    and
    (a - b)/d = p - q is a natural number.
    Dus (a - b) has a factor d.

Proof 2.
    assume:
    a - b = d.p and b = d.q
    Then:
    a = d.p + b = d.p + d.q = d(p + q)
    or :
    a has a factor d.
    b has a factor d.
    so:
    a and b share a common factor d
    Conclusion: a common factor of a - b and b is also a common factor of a and b.
    No factor can be added.

Example:
Repeated application of the Euclid theorem, calculation of GCD(110901,35553):
    110901 = 3 * 35553+4242
    35553 = 8 * 4242+1617
    4242 = 2 * 1617+1008
    1617 = 1 * 1008+609
    1008 = 1 * 609+399
    609 = 1 * 399+210
    399 = 1 * 210+189
    210 = 1 * 189+21
    189 = 9 * 21+0
we see:
    GCD(110901,35553) = 21

Applications
LCM
1.Adding fractions with unequal denominators.
1
85
 + 
1
119
 = 
1
5 · 17
 + 
1
7 · 17
 = 
7
5 · 7 · 17
 + 
5
5 · 7 · 17
 = 
12
595

2.coincidence of periodic events.
Two city busses A and B depart at the same time from a bus station.
A needs 70 minutes to return, for B this is 50 minutes.
In LCM(70,50) = 350 minutes they meet again at the bus station.

 GCD
1.Place factors in terms outside parenthesis (smallest packages)
2475 a + 1950 b = 3 2 · 5 2 · 11 a + 2 · 3 · 5 2 · 13 b = 3 · 5 2 (3 · 11 a + 2 · 13 b) = 75 (33 a + 26 b)

2.reduction of a fraction.
1950
2475
 = 
2 · 3 · 5 2 · 13
3 2 · 5 2 · 11
 = 
26
33

Questions
a. what are the first 10 multiples of 23?

factorize:

b. 12
c. 150
d. 375
e. 147

calculate:

f. LCM(150,375)
g. LCM(147,375)
h. GCD(150,375)
i. GCD(147,375)

A company has 34650 jars with strawberrie jam and 36300 tins with fish.
They must make as much packages as possible each containing the same number of jars and tins.

j.how many packages are this and what are the contents of such a package?

Three connected pinwheels have 24, 30 and 40 pins.
Each pinwheel has a (arrow) sign.

k.how many pin positions these wheels have to move until the arrows point in the original direction?

Tiles are sized 56 * 98.
Using these tiles we need to cover a square area.

l. what is the smallest size of such a square?

m. what is the size if the tiles are a * b (length * width) in size?

n. investigate if 5419 is a prime number.

o. is 4587 prime?

p. is 62809 prime?

See drawing:
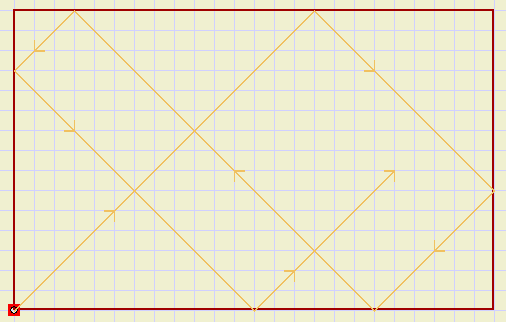    room with mirrors on the walls and a light source
The beam finds it's way from wall to wall.

q. how many squares does the beam cross until it reaches it's source again?
(room has 24 * 15 squares)

r. how many squares if the room size is a * b (squares) ?

In case you know some more math, including roots:
Imagine you have to calculate a table with the roots of all numbers from 1 to 1000.
Say the accuracy is 3 decimals. Calculation of all roots is very much work.
However, considering the rule
\a b
 = 
\a
 
\b
much work may be saved.

s. explain how.

A rectangle size 585 * 825 cm2 must be split in equal squares.
(count in cm. no fractions)

t. what is the size of the biggest possible square?

u. what is the number of squares?



Answers:
----------------
a. 23 46 69 92 115 138 161 184 207 230
b. 22.3
c. 2.3.52
d. 3.53
e. 3.72
f. 750
g. 18375
h. 75
i. 3
j. 1650 * ( 21 jam + 22 vis)
k. 120
l. 392
m. LCM(a,b)
n. yes
o. no
p. no, 107 * 587
q. 240
r. LCM(2a,2b)
s. calculate only roots of primes
t. 15
u. 2145
-------------------