geometric proofs of trigonometric identities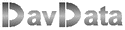

Introduction
Below, some proofs are presented of trigonometric identities.
The proofs do not use any trigonometric formula or rule, what makes them quite special.

Identity Nr. 1
    arctan(
    1
    2
     ) + + arctan(
    1
    3
     ) = arctan(1 )
Proof A.
See figure 1. below.
Pictured are 4 squares.
    fig.1

Since:
    LC1 = arctan(
    1
    2
     )
    LD1 = arctan(
    1
    3
     )
    LB1 = arctan(1 )
We must prove:
    LC1 + LD1 = LB1.........1)
DEMC ~ DDAE, because:
    1. LA = LM = 900
    2. MC = 3.ME
    3. AD = 3.AE
so:
    LE1 = LD1
which changes ........1) into:
    LC1 + LE1 = LB1
This is a basic geometric theorem.
(remember: 1800 - LB1 = 1800 - (LC1+LE1)
This concludes proof A.

Proof B.
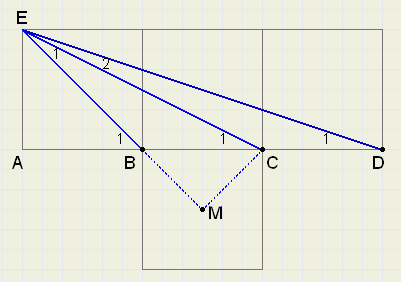
See figure 2. below:
    fig.2

Note: EF = 5, because of theorem of Pythagoras.

DADG is the rotation of DABE over 900= LGAE.

Now observe polygon AEFG.
    FG = FE
    AG = AE
so:
    DAFG and DAFE are congruent
so:
    LGAF = LFAE = 450
    LGAD + LDAF = 450
    arctan
    æ
    1
    3
    		ö
    ­­
    èø
     +  arctan
    æ
    1
    2
    		ö
    ­­
    èø
     =  arctan 1
Which concludes proof B.


Identity Nr. 2
    sin(200 ) + sin(400 ) = sin(800 )
Proof.
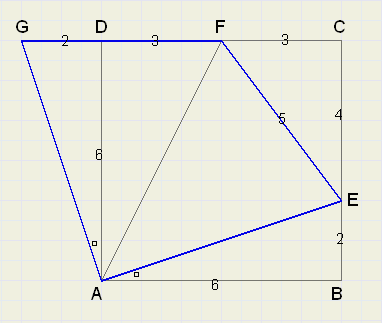
See figure 3. below:
    fig.3

M is the center of a circle with radius = 1.
Points A,B,C,D are located on the circle at the indicated angles.

Chord DC is extended by CE = BC.
Now DCBE is equilateral because:
    LDCB = 0.5(3600 - 1200) = 1200 .........(see appendix 1.)
    LECB = 600 ....so
    LCBE = LCEB = 600....so
    BE = BC = AB
and we see:
    DDBE is congruent to DDBA....so
    DE = DA ............and since
    CE + DC = DE
    AB + DC = AD
    2sin(200 )+ 2sin(400 ) = 2sin(800 )........(see appendix 2)
    sin(200 )+ sin(400 ) = sin(800 )
and we have proved the 2nd identity.

Appendix 1 (measuring angles by arcs)
See figure 4. below:
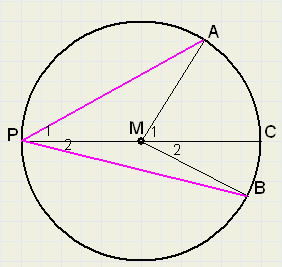    fig.4

By:...... arc AB = 800 we mean : LAMB = 800

Since
    LM1 = LA + LP1.......exterior angle of DPMA
    MA = MP
    LP1= LA
    LM1 = 2*LP1
    LP1 = 0.5*LM1 = 0.5* arc AC.....2
.....1 and .....2 combined:
    LP1,2 = 0.5*LM1,2 = 0.5*arc AB
In words:
    an angle located on a circle is half the size of the associated arc.


Appendix 2 (sine and chord relation)
See figure 5. below:
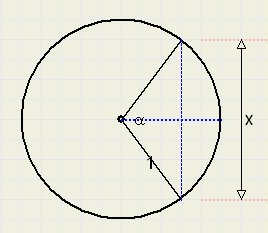    fig.5
    sin
    æ
    a
    2
    		ö
    ­­
    èø
     = 
    x
    2
    x = 2 ·  sin
    æ
    a
    2
    		ö
    ­­
    èø