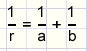Geometry problem solutions (11..20)
11.
Given is triangle ABC with inside point P. See next figure for details:



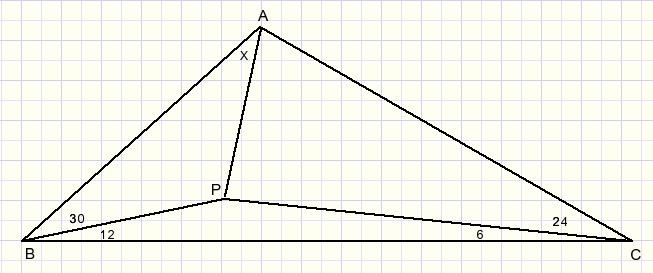
Question: the size of angle x.

Problems like this may be attacked by trigonometry: cosine and sine rules.
Just give some side a convenient value and calculate the other sides and angles.

However, the regularity of this figure (angles are 30 degrees, all multiples of 6)
suggest that a pure geometric approach might work.

This problem is not easy.
We notice point P where lines from angles A,B,C intersect.
For a start we think about a more familiar situation.
The bisectors of the angles of a triangle intersect at 1 point.
Maybe the problem can be modified to create bisectors.
Let's draw the circumscribed circle of ABC:



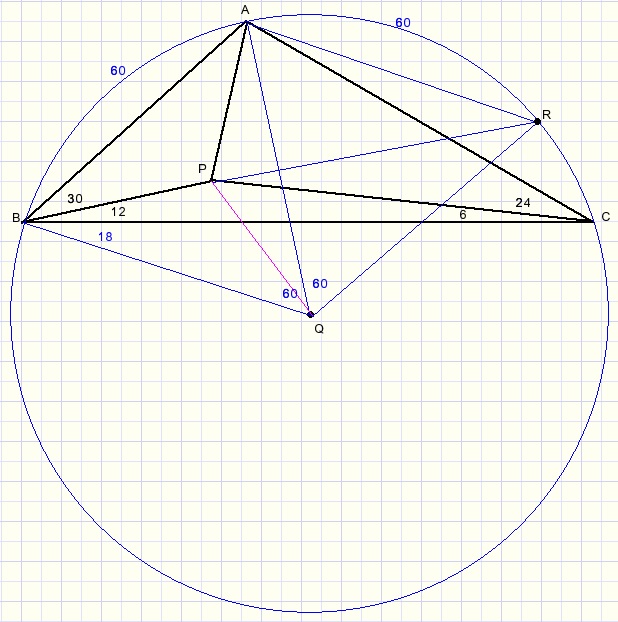
The center of this circle is Q, we draw QB, QA and QR.
R is on the extension of line BP.
Application of the Thales theorem for angles B, C reveals:
(see appendix 2 for explanation)
    - arc AB = arc AR = 60 degrees.
    - triangles ABQ and AQR are equilateral.
    - ABQR is a rhombus so AQ and BR are perpendicular.
    - PA = PQ (symmetry).
    - LCBQ = 18 degrees.
    - BP is bisector of LB.
Next we add the circumscribed circle of triangle APC.
The picture below is correct if LPAV = 90 degrees,
in that case PV is diameter.



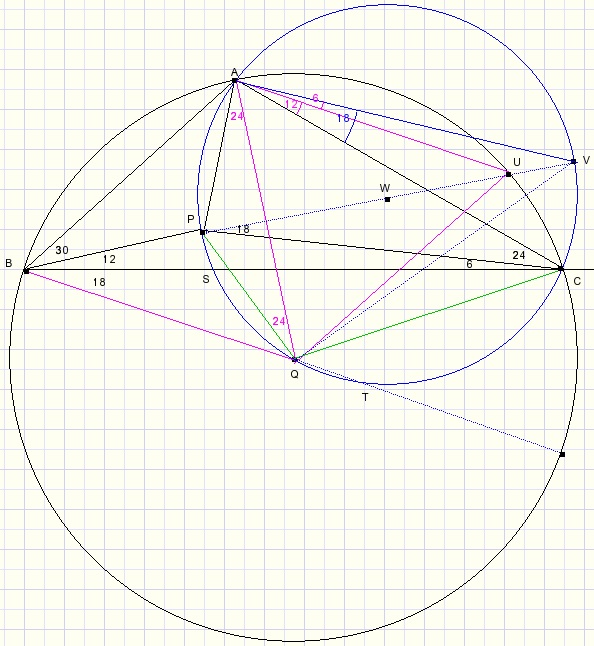
    - LCAU = LPBC = 12 (arc UC = 24)
    - LCAV = LVPC = 18 (arc VC = 36)
    - LVAU = 18 - 12 = 6
    - LPAQ = 24 (arc PQ = 48)
    - LPAV = 24 + 60 + 6 = 90 degrees.


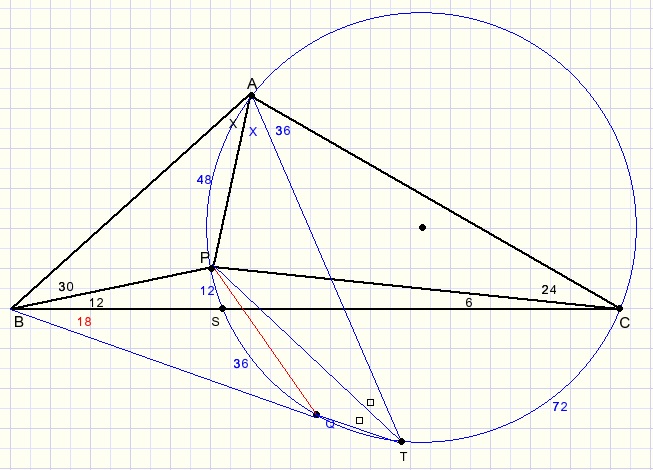
LATP = LPTQ = 24 degrees.
PT is bisector of LT.

LCBT = 18 = (arc CT - arc QS)/2, so arc CT = 72 and LCAT = 36.

The bisectors intersect at 1 point (P) so AP also must be bisector.
LA = 180 - 42 - 30 = 108 degrees.
2x + 36 = 108
x = 36.

Appendix 1

Trigonometric calculation of x:

steps
    1. let AB=1.
    now calculate:
    2. BC with sine rule.
    3. BP with sine rule.
    4. AP with cosine rule.
    5. x with sine rule.



Appendix 2

The theorem of Thales. (Greek mathematician 624 - 547 before Chr.)

Measuring angles with arcs:
definition:
    the size of an arc means: the size of the corresponding angle at the center of the circle.


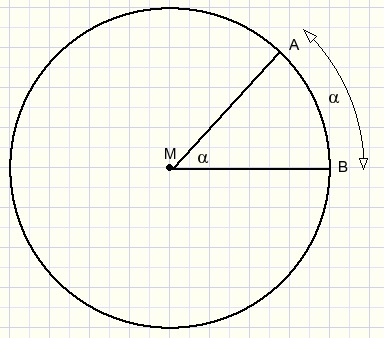
theorem
    an angle on the circumference of a circle is half the size of the arc.


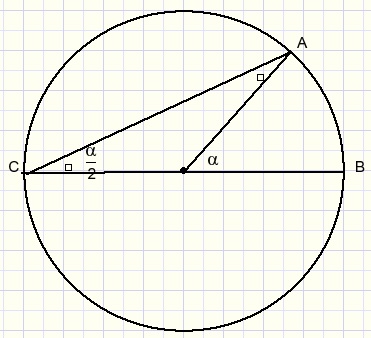
Angle C is half the size of arc AB.
The proof follows from isosceles triangle AMC and the rule that
the exterior angle of a triangle equals the sum of the opposite interior angles.
This theorem is true for all situations, which follows from addition and subtraction of arcs.



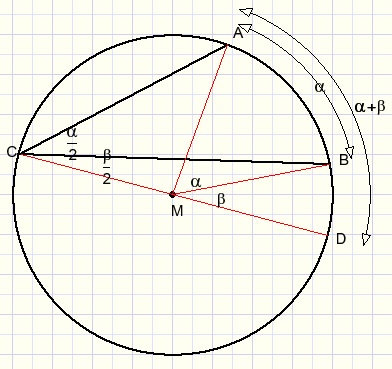
By applying the Thales theorem we can unveil rules for angles inside and outside a circle as well.



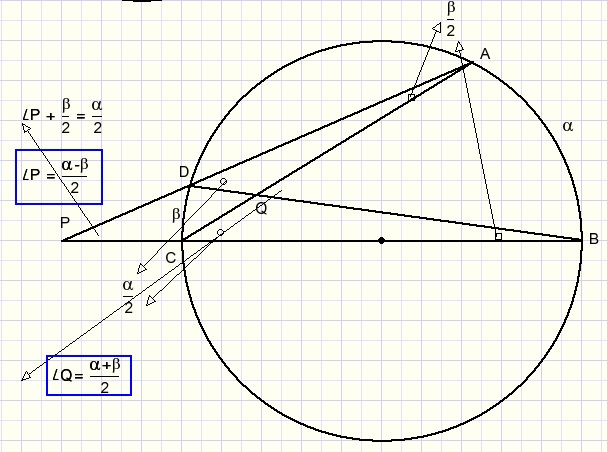
    - an interior angle is equal to half the sum of both arcs.
    - an exterior angle is equal to half the difference of both arcs.
Shown is the easy case where one edge is diameter.
Addition or subtraction of arcs shows that these rules are true for all situations.
12.
In the figure below we notice right-angled triangles and their inscribed circles.



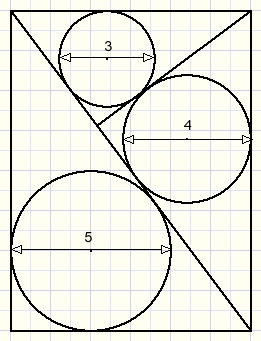
Question: what is the area of the rectangle for these inscribed circle diameters?

Please look at the picture below:



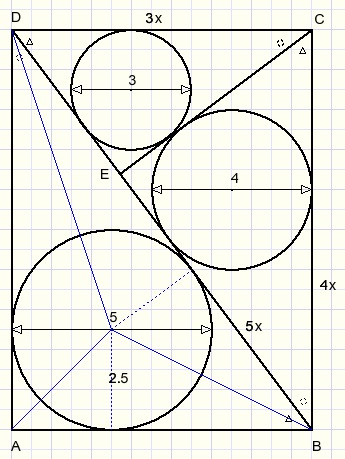
Triangles DEC, CEB and BAD are similar.
See equal angles marked by the same symbols.
Affine lines in the triangles have the same ratio.
So we know that the hypothenuses have ratios 3:4:5,
the same as the diameters of the inscribed circles.

Now define:
    AB=3x
    BC=4x
    BD=5x
which is in accordance with the Pythagoras lemma.

The inscribed circle of triangle ABD has a radius of 2,5.
The area of triangle ABD is (base x height / 2)
    0,5 . 2,5 . 3x + 0,5 . 2,5 . 4x + 0,5 . 2,5 . 5x = 15x.
The area of triangle ABD also is:
    0,5 . 4x . 3x = 6x2
from
    15x = 6x2
follows
    x = 2,5
The area of rectangle ABCD is:
    3 . 2,5 . 4 . 2,5 = 75


Appendix




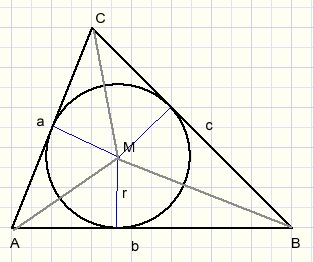
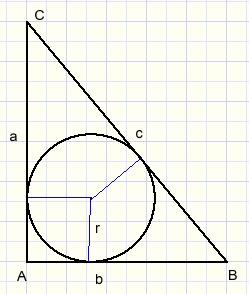
Writing the area of triangle ABC as [ABC]
we find for the radius r of the inscribed circle (see picture above):
    0,5ra + 0,5rb + 5,5rc = [ABC]
so:



Could this formula be simplified given that LA = 900?
In that case we know:
    a2 + b2 = c2
    2[ABC] = ab


Let's go:


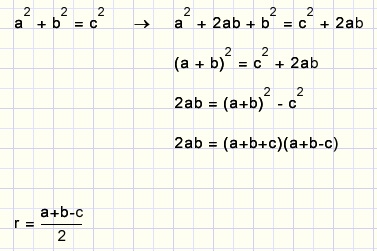
13.
This geometry puzzle was found in Facebook group "Classical Mathematics".
Solutions are partly my own.



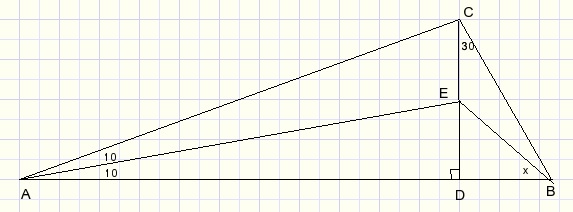
Question : calculate angle x.

Several approaches exist.

1.Goniometric + calculator

This is the most simple way.
Let BD = 1.
So:
DE = tan(x)
DC = tan(60)........1)
DE = AD.tan(10).......2)
DC = AD.tan(20).......3)

combining:



Calculator:
DE = 0,839099631
x = arctan(0,839099631) = 40

2.Goniometric without calculator

DE = tan(40)
Multiply in the last equation 1) numerator and denominator by tan(40)
Now this must be true:
tan(60).tan(10) = tan(20).tan(40), after division tan(40) remains.

Geometric picture:



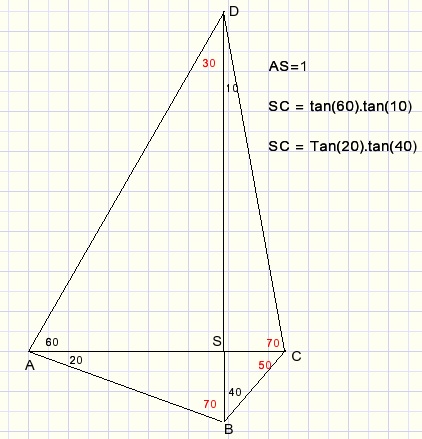
Look at quadrilateral ABCD above.
Known angles are pictured in black.
Triangles ASD, ASB, CSD may be constructed.
But a question remains: what are the angles of triangle BCS: 40 and 50 degrees?
Who helps?

3.Geometric solution

Look again at the first picture.
Edges of lines AC, AE are extended to make isosceles triangle ABG.
AF is perpendicular bisector of BG.



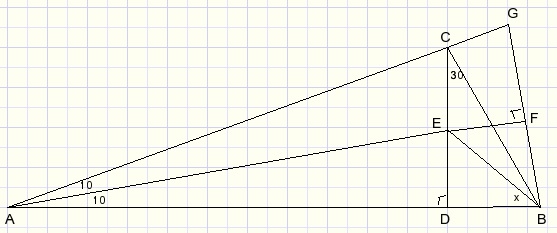
LFEB = x+10..........{exterior angle of ΔABE}
For reasons of clarity a part is lifted out and enlarged:



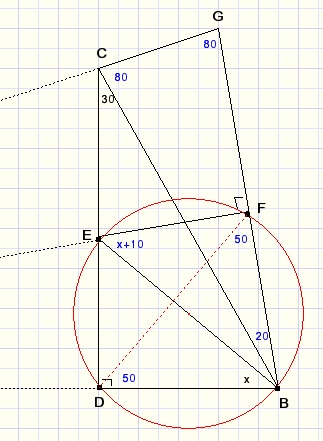
2DB = BG....{because LDBG=60}
2BF = BG....{because F is center of BG}
so:
BD = BF
LDBF=80
LBDF=LBFD=50

Construct the circumscribed circle of quadrilateral DBFE....{BE is centerline because 90 degree angles D and F}
LFEB=LFDB....{both on arc BF}
x+10 = 50
x = 40
14.



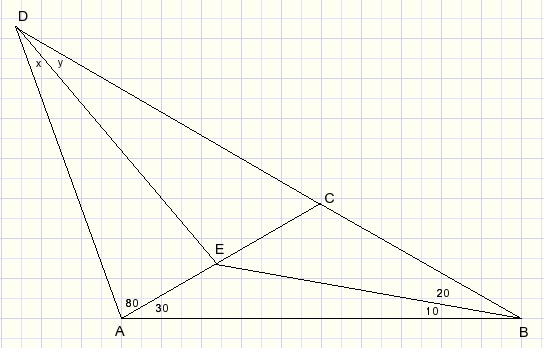
Asked: find angles x, y at point D in above picture.

Solution

Draw a circle with center E and radius EB.
Extend some lines, see picture below.



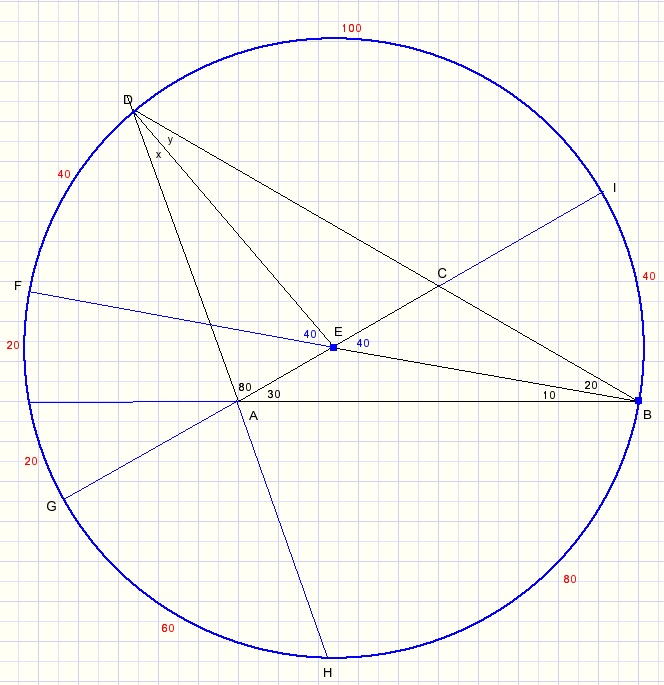
It seems that point D is part of the circle.
That's what we have to prove.

Please look at ΔABE.
LLEB = 40 because of being an exterior angle.
Arc BI = 40 = arc FG.
LCBE = 20....arc FD = 40.
LDEI = 100 = arc DI.
LDAC = 80 = (arc DI + arc GH)/2....arc GH = 60.
arc HB = 360 - (40 + 100 + 40 + 20 + 20 + 60) = 80.
Look at ΔABD.
x + y = 180 - (110 + 30) = 40.
Point D is part of the circle because LD is 40 degrees and spans arc HB = 80.
Because DE = EB, LBDE = 20 = y = x.
15.
Calculate x in next picture.



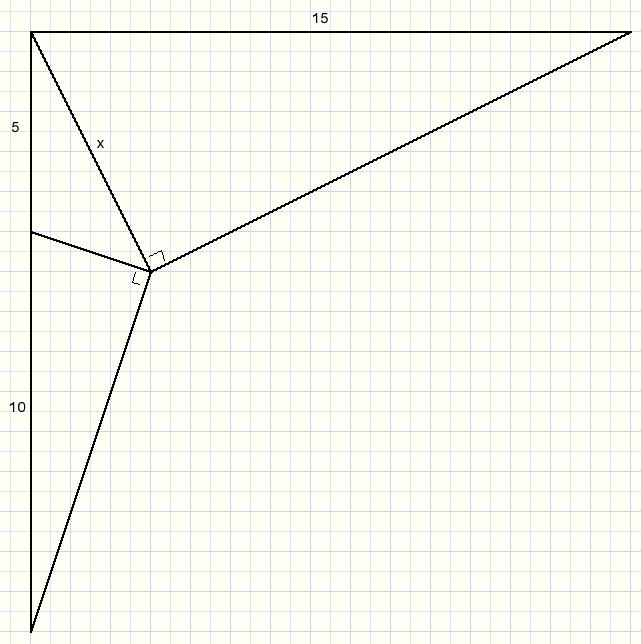
Solution:



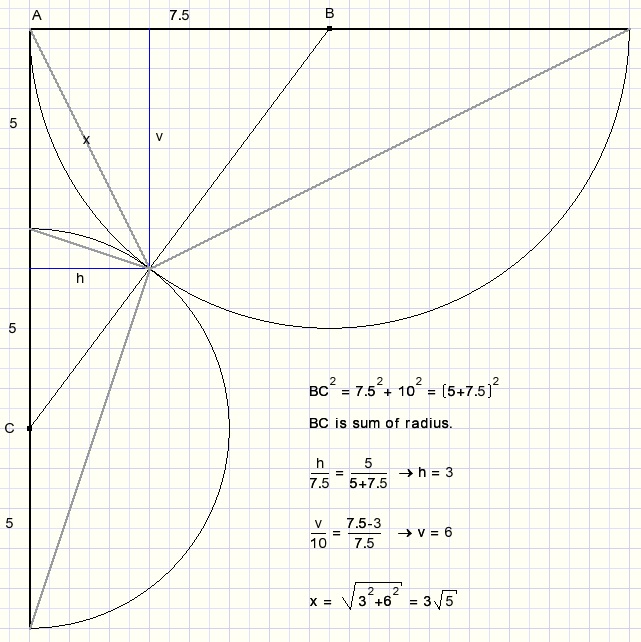
Draw half circles with centers B and C.
These circles share 1 point, so BC is the sum of their radius.
Now apply the rules for similar triangles to calculate h and v.
Next apply the Pythagoras lemma to calculate x.
16.
Below is pictured rectangle ABCD with BD perpendicular to CE.
Prove that BE x BA = (BC)2.



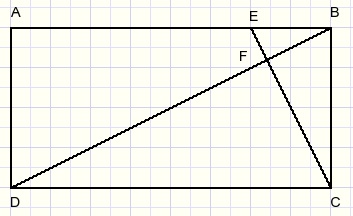
This reminds us at the "power of a point relative to a circle".
First I present some theory.

The power of a point relative to a circle

From arbitrary point P outside a circle we draw a line that intersects the circle at points A and B.
Now we notice a remarkable thing:
the product PA x PB is the same for every line.
This product we call "the power op P to the circle".



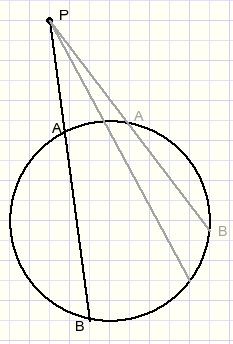
Proof



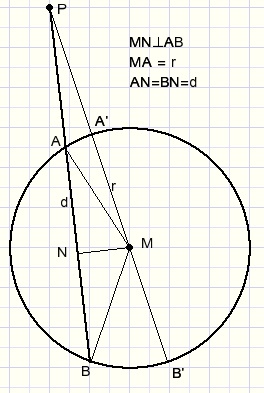
    PA.PB = (PN-d)(PN+d) = PN2 - d2.....1)
    PN2 = PM2 - MN2.....2)
    MN2 = r2 - d2.....3)
    ..2) + ..3) :
    PN2 = PM2 - r2 + d2.....4)
    ..1) + ..4):
    PA.PB = PM2 - r2 + d2 - d2 = PM2 - r2 = (PM-r)(PM+r) = PA' . PB'
Product PA'. PB' is constant.

Solution 1

We notice the circle defined by points A, E and C and the power of B to this circle.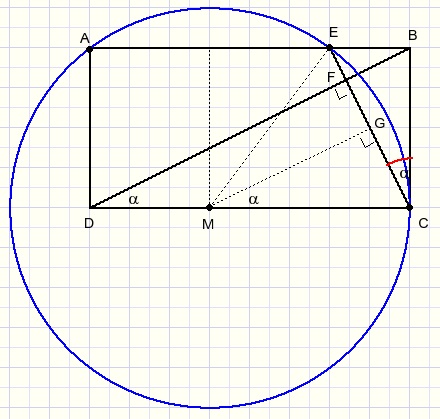



BE.BA = BC2 if BC is tangent to the circle so:
The center of the cirlcle is on line CD.

M is the intersection of the perpendicular bisector of AE with CD.
Draw MG perpendicular to CE.
MG is perpendicular bisector of CE by congruence of triangles MGE and MGC.
M is the intersection of perpendicalar bisectors so is the center of the circle.

The poper of B tot the circle is fixed so: BE.BA = BC2.

Solution 2

This proof uses the properties of similar triangles.
See picture below.



17.
In picture below AD = DC
LABC = 45 deg.
Question: find angle x.



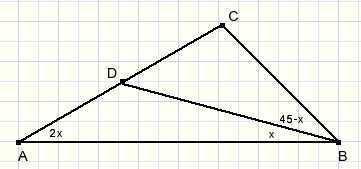
Solution
Draw circle with center D and radius AD.
E is intersection of AB with circle.
Draw line CE.
Draw line DE.



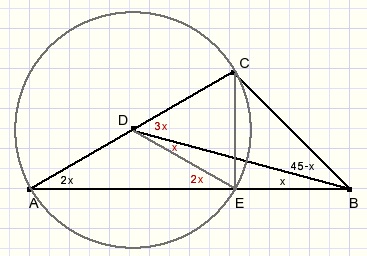
LAEC = 90....... {spans circle arc of 180 deg.).
LBCE = 45 .....so.. BE = CE.
LAED = LDAE = 2x.
LCDE = 2x + 2x = 4x......{exterior angle of triangle AED}.
LAED = 2x = x + LBDE.....LBDE = x.....DE = BE.
Conclusion:
CD = DE = EC.
Triangle CDE equilateral.
LCDE = 4x = 60.
x = 15 deg.
18.
The question is to calculate angle x.



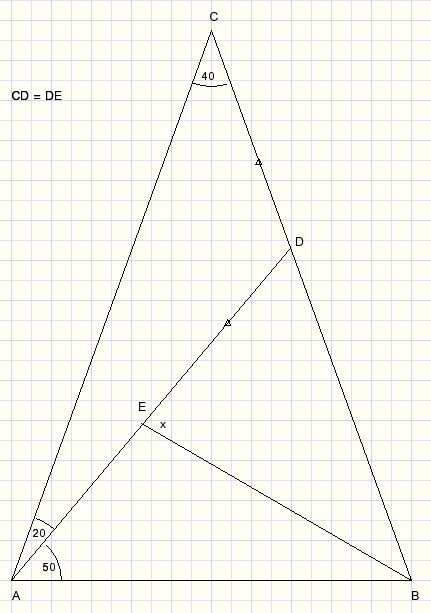
ΔABC is isosceles, AC = BC, because LB = LA = 70.

Point D is the center of the circle through C and E.
This circle intersects BC in point H.
Draw lines CE and EH.
Draw perpendicular bisector of AB.
Draw point G on CF such, that HG is perpendicular to CF.



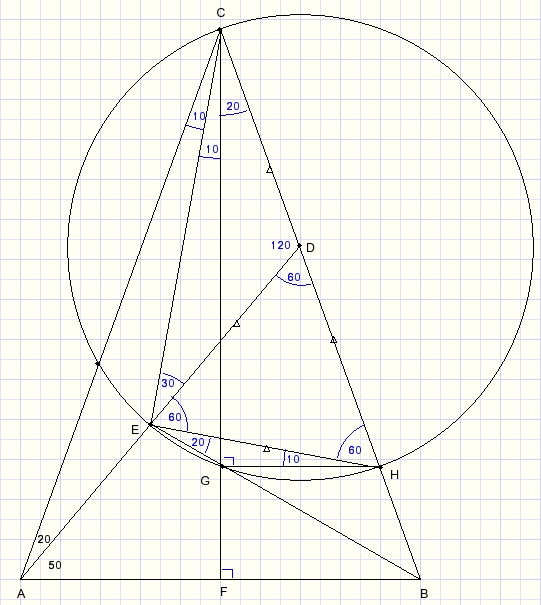
Now look at ΔADC.
LADC = 180 - 20 - 40 = 120
LADB = 180 - 120 = 60.
DE = DH so LDEH = LHED = (180 - 60)/2 = 60.
G is on the circle because LCGH = 90.

LHEG = LBCF = 20 because both span arc GH.
x = LDEB = 20 + 60 = 80.

This leaves the question: is point G on line BE?
LAEB = 180 - 60 - 20 = 100.
LABE = 180 - 100 - 50 = 30.
LFGB = 90 - 30 = 60.
LCGE = 120/2 = 60 because it spans arc CE.
So point G is on line BE.
19.


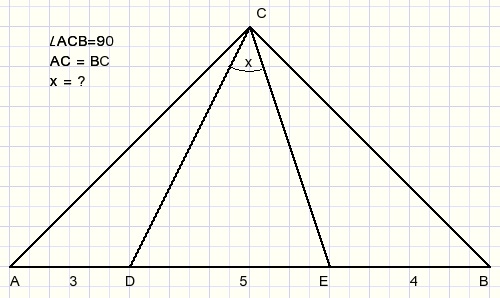
Problem:
Above we see isosceles right angled triangle ABC.
Proof that angle x = LDCE = 45 degrees.

The lengths AD=3, DE=5 and EB=4 show a Pythagoras triple.
So we approach this problem in a more general way:
If AD=a, DE=c and EB=b and also a2 + b2 = c2
then prove that x = 45.

The proof

Shift lines AD and EB parallel to AB until they meet at point E.
Because of similarity of ΔABC and ΔDEM (equal angles) MD = ME.
We prove that also MC = MD = ME.



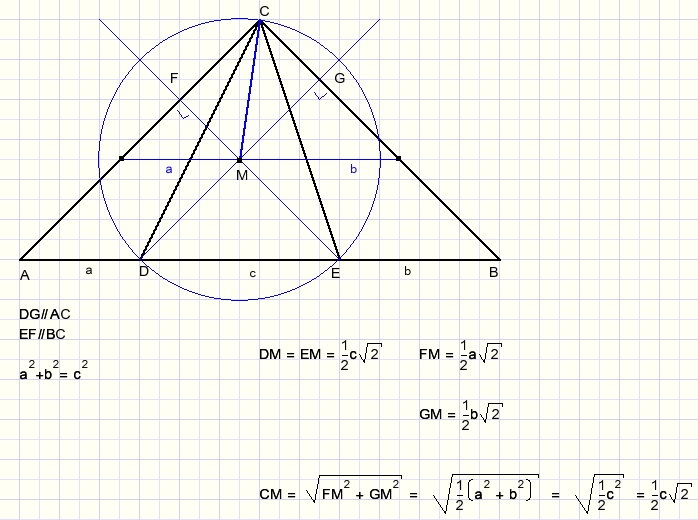
Note: in a right angled isosceles triangle with a hypothenuse of a, the other sides are
half the root of a.

M is the center of a circle through points D, E and C.
LDME spans arc DE of 90 degrees.
Angle x also spans arc DE so LDCE = 45.
20.
Given are:
A 180 degree circle arc with center P and radius c.
Within two other half circles with centers M, N and radius a ,b.
c = a + b.
Within also two small circles with radius r which touch the other circles and line AB.
AB is tangent of the inner circle arcs.

Asked:
Express r in a and b.



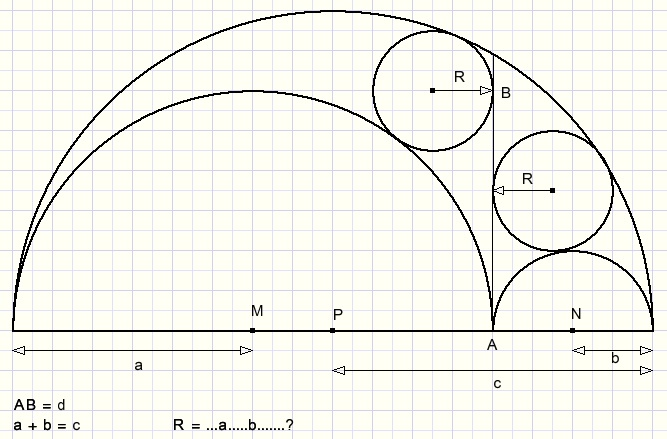
Please look at the next picture:



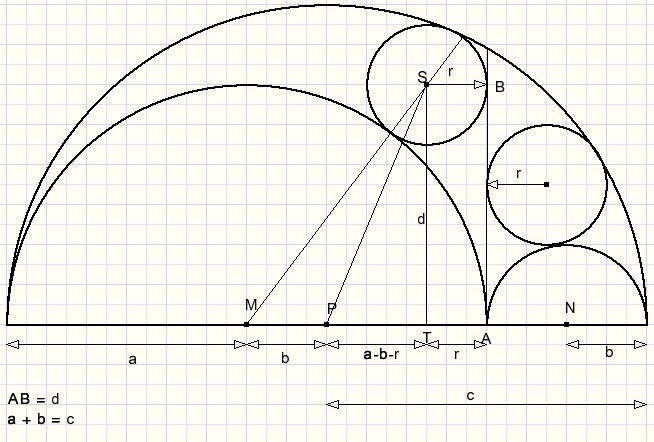
We calculate distance d = ST twice:
- for ΔPTS
- for ΔMTS

Then these distances are equated equal.



After simplifying the equation r appears to be the harmonic mean of radius a and b.
We also may write: