a wysiwyg math editor

a WYSIWYG math editor (1)

to part 2

Introduction

This article describes the basics of a text editor for mathematical documents.
This editor does not use scripts: text is directly typed into the document
and other text elements are directly selected from a menu.
This makes it a so called WYSIWYG (What You See Is What You Get) type editor.

The editor handles the following subjects:

This article focusses on the text part.
The description is at block diagram level and is not programming language specific.

At first some examples:

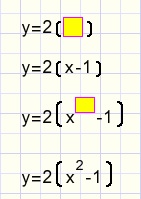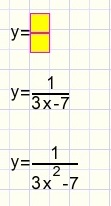Left we typed y=2 and add a parenthesis element (...) with an empty line (yellow).
On this line we type x-1 .
Then we add a power element after the x and type a 2 in it's line.
The parenthesis adjust their position and hight automatically.

Right y= is typed and a fraction element is added.
In the numerator line we type 1 and in the denominator 3x-7.
After the x a power element is added, it's line is filled with a 2 to square the x.
When the denominator changes, the numerator adjusts it's position.
The fraction line expands automatically just as the vertical position of the denominator.

Another example:

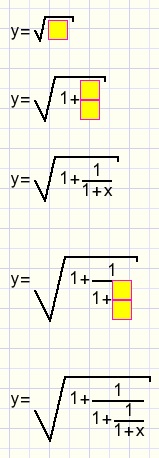y= is typed and a root element is added.
In the root's line 1+ is typed and a fraction element is added.
The lines of this fraction we fill with 1 and 1+x.
Then the x is replaced by a fraction element.
The lines of this element are again filled with 1 and 1+x.

We notice that the root changes it's shape as the contents grow.

Basics

The document is comprised of elements. An element occupies a rectangular area.
Elements are coded by numbers. From these numbers the image is calculated at paint time.
These are the types of elements:

The characters are derived from the "XFont", a homebrew font with:

Macro's contain one or more lines and sometimes graphical elements such as fraction lines
or roots.

Structures may become pretty complex so strict rules are required.
The implementation is rather abstract.

Some operations are the responsibility of the individual element, other operations apply to
all element types in general.
These are the responsabilities of an element:

The character element

Picture below shows a line and two characters.
The characters are the children of the line. The line is the parent of the characters.
The parent must calculate the position of it's children, relative to itself.

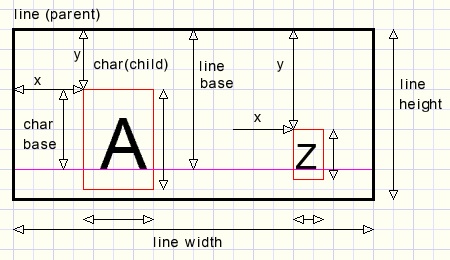
Lines, macro's and characters have a so called base.
A line places characters with their base on it's own base.
That takes care of vertical alignment.
A line left aligns it's children: characters and macro's.
Then it calculates it's width and height.

The advantage is that repositioning of an element does not affect the children.

An element may never calculate it's own position. This is the responsability of the parent.

Macro's

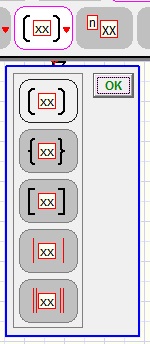
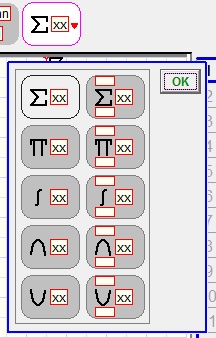
Macro's make the editor a true math editor.
Below is the macro menu, more will be developed

A macro has one or more lines as child and sometimes also graphical symbols as in the case
of fractions or roots.
These graphical symbols are not coded but calculated at paint time by the element.

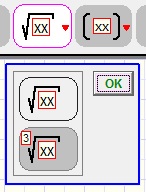
Some macro's require additional choices, indicated by a small red triangle sign.
A right mouseclick on the menu button unfolds the popup submenu:

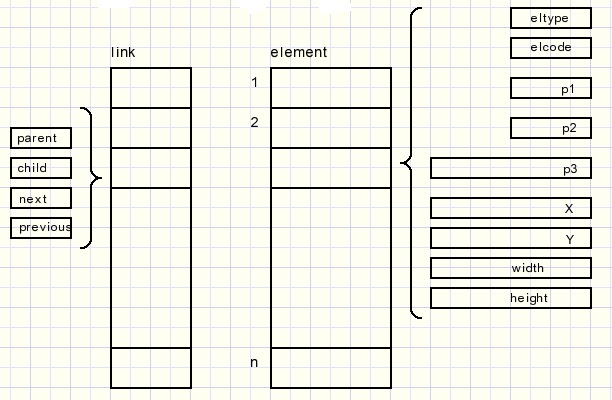
Coding, Parents en Children

A parent may have an unlimited number of children.
A parent points to the first child, each child points to the next by the number next
and to the previous by the number previous.

Parent, child, next and previous are element numbers and define the structure.

The element properties are coded in a record of type Telement.
The complete document is an array of records of type Telement.
Parent,child,next and previous make a record of type TLink.
For each element there is a Tlink record.

There is no direct acces to the links[ ] array.
Changes to links are done indirectly by procedures.
The UNDO system is also implemented here.
Edit operations amount to making changes in array links[..].
Changes concerning fonts or styles require changes in the elements[..] array.

The fields elType,elCode,p1 and p2 are of type byte, the others are of type word.
p1,p2 and p3 are element dependent.
In most cases p1 is the font (pointer to font table), p3 is the baseline position.

The Link fields are of type dword (32 bit unsigned integer).

Element 1 is the complete document. Element 1 has no parent.
All other elements are children (of children of children...) of element 1.

If an element changes shape, the parent is forced to recalculate itself.
This implies recalculation of the position (x,y) of the children.
If the parent's dimensions change also, the parents parent is called for recalculation.
That's the complete principle.

Another example: de ABC equation ax² + bx + c = 0 and it's roots:

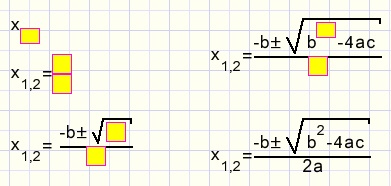
After the x an indices macro is added and it's line filled with 1,2
after the = character a fraction element is added, after +/- a root macro
and after the x a power macro.
At no time I had to take care of alignment. It was all done automatically.

Another example, made in just a few seconds:

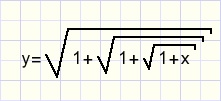
Here is the tree structure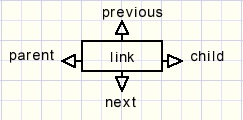

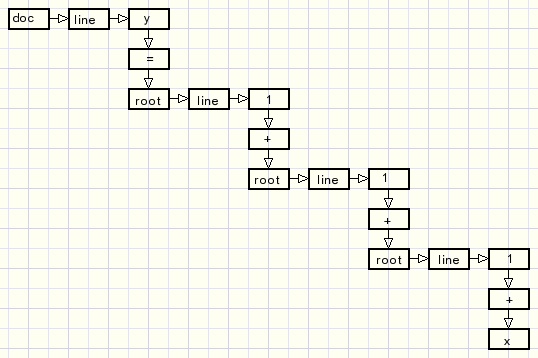
Final example:

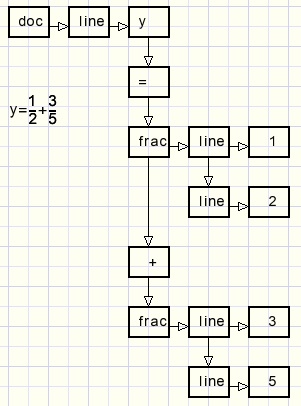
Postscript

The general idea is not difficult.
However the Delphi code has some complicated parts because the operations are rather abstract.
At present the structure is defined but much work has to be done.
Some more macro's are needed.
Cursor movement still is primitive, many more editing capabilities have to be implemented.
The work will be continued.

In a next article I may go into more details.