Nim games
download Nim program

Nim game program




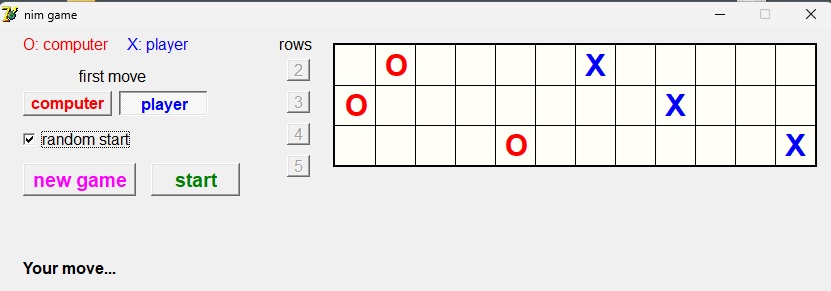
The program is single player.
Computer and player alternately shift a stone of their color any number of places left or right.
Stones may not cross.
Winner is who prevents the other player to move by clamping.

Select number of rows by pressing a row button.
Select first move by computer or player.
Select random start position or else O’s at left and X’s at right position.
Press the [new game] button to place O , X stones.
Press [start] to play.

After pressing [new game] the program is in SETUP mode.
This allows for reposition of the stones.
A left mouseclick on a field moves the X stone to that field.
A right mouseclick moves the O stone.

After pressing [start] move a blue X stone by mouseclick on the destination field.

General introduction to Nim games

Nim games are a category of board games with very different appearance but with a common strategy,
properties and math.
Two players alternately shift or remove stones until a player is unable to move.
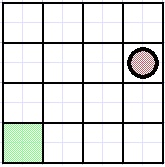
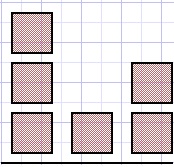
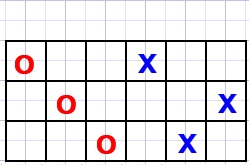
Picture below shows three type of Nim games

fig1afig1bfig1c

Fig1a
Players alternately move the stone any places either left or down.
Winner is who places the stone in the leftmost down (green) field.
The position of the stone is (3,2), the winning green field is (0,0,0).

Fig1b
Players alternately remove any amount of stones from one pile.
Winner is who removes the last stone(s).
Game position is (3,1,2), the number of stones in a pile counted left to right.

Fig1c
Players (red, blue) alternately shift one stone of their color any columns left or right.
Stones may not cross.
Winner is who clamps the other player, who is unable to move.
Game position is (2,3,1), the number of empty fields between the stones in a row.

Note: game a is two dimensional, games b and c are three dimensional.
Any number of dimensions per game is possible.

Nim game characteristics

There are two players. In this Nim project one player is the computer.
A board position is either good or bad.
A position is good when any move results in a bad position.
A position is bad when a move exists which results in a good position.

To find all good board positions start with winning position (0,0,0) for a three dimensional game.

So positions like (5,0,0) or (0,3,0) are bad because a single move may result in postion (0,0,0)
Next good positions are (1,1,0) , (1,0,1) and (0,1,1) being 2 moves away from good position (0,0,0).

This Nim game program uses the type c games with 12 columns and rows selectable from 2..5
To find all good positions a program (NimResearch) is written.

Nimresearch project

Next picture is output of Nimresearch showing good points of a three dimensional game type c with 8 columns.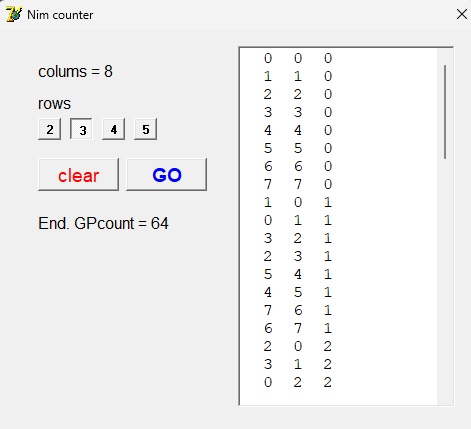



64 good positions are found of which some are listed.
The numbers indicate the empty fields between the O..X stones per row.

The Nimresearch program calculates good board positions in a numerical way.
Starting at winning position (0,0,0) for a (c type) game with three rows,
the next good positions are two moves away from (0,0,0) so are (0,1,1) (1,0,1) (1,1,0)
Good positions are stored in array GoodPoints[..] {column per row}
Array counter[1..5] {maximal 5 rows} counts columns in each row.
This counter is incremented by: 
function CounterInc : boolean;
var carry,i : byte;
begin
 carry := 1;
 for i := 1 to rowcount do
  begin
   counter[i] := counter[i] + carry;
   if counter[i] < columns then
    carry := 0 else counter[i] := 0;
  end ;
 result := carry = 0;
end;
Next procedure tests each value of the counter for a good position
which means being two moves away from earlier found good position.
procedure TestPoint;
var i : word;
    d,j : byte;
begin
 i := 0;
 repeat
  inc(i);
  j := 0;
  d := 0;
  repeat
   inc(j);
   if counter[j] <> GoodPoints[i,j] then inc(d);
  until j=rowcount;
 until (d=1) or (i=GPX);
 if d <> 1 then savePoint;
end;
Note: GPX is the number of good positions stored so far.

Conclusion

After observing the Nimresearch output we see the simple trick:
to calculate winning board postions:
    - write the board position (X,Y,Z) in binary
    - for a good postion X xor Y xor Z = 0.

Analytical proof

The game positions are written as groups (G0,G1,G2...)
G0 : 0,1 position in (2*2) group
G1 : 0,1 position in (4*4) group...
G2 : 0,1 position in (8*8) group etc.

For a 2 dimensional G0 group good positions are (0,0) and (1,1).
For G1, G2.. groups the same rule applies: Good groups always are (0,0,) and (1,1).

For a good position all G0, G1, G2.. groups must be good.



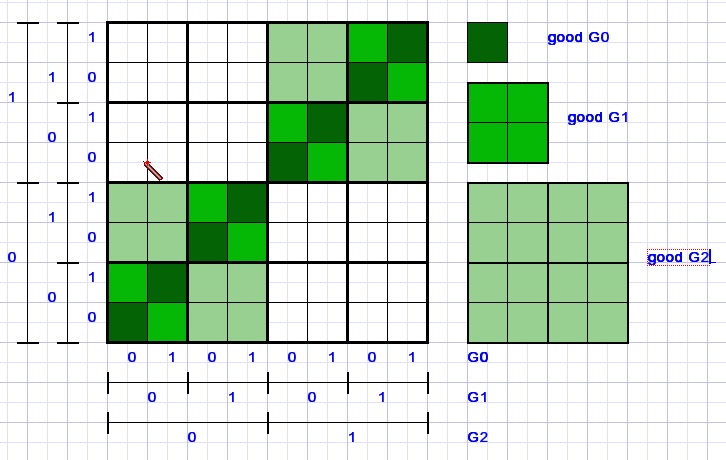
Counting decimal the position (6,6) binary (110,110) is good.
G0 = (0,0) G1=(1,1) G2=(1,1) which are all good groups.

Position (2,6) binary (010,110) is false because G0=(0,0) G1=(1,1) G2(0,1)
G2 is wrong (left top 4*4 group in above picture)

For three dimensions, the winning position is (0,0,0).
In a 2*2*2 group G0 good positions are (1,1,0) (1,0,1) and (0,1,1).
But this is true as well for G1, G2..groups.

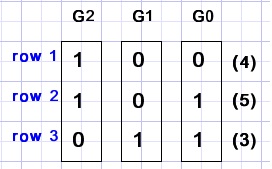
Is (4,5,3) a good position?

(4,5,3) is binary (100,101,011)
G0 = (0,1,1) OK
G1 = (0,0,1) wrong
G2 = (1,1,0) OK conclusion: bad position.



Next good positions are obtained by adding good groups:
Let G0 = (1,1,0) and G1 = (0,1,1)
G0 + G1 = (.1, .1,.0) + (0.,1.,1.) = (01,11, 01) decimal (1,3,2)

Note: while adding groups shift G1 position left 1 place, G2 position by 2 places etc.

The Nim game project

Data formats

var GPos : array[1..2,1..5] of byte;  //1,2:computer,player; 1..5: row; value is column
    Game : array[1..5,1..12] of byte; //0:empty; 1:computer; 2:player                                
    rowcount : byte = 2;
    Gmap : Tbitmap;
    CHmap : array[0..2] of Tbitmap;
    movebusy : boolean; //prevents interruption of moving  
                        //stone

Painting

Fields are 40*40 pixels.
The game edges are painted on the canvas of form1.
All painting is done in bitmap Gmap.
Parts of Gmap are copied to paintbox1 on form1.
Reason is to avoid a flickering display which occurs when paintbox1 is erased.
During a move O and X stones move pixel by pixel which is controlled by the CPU clock.
A stone shifts 1 pixel per 3 milliseconds.
This cannot be controlled by the millisecond clock because this clock only updates once per 15 millisecs.

The O anx X stones are initially painted in bitmaps CHmap[1] and CHmap[2].
Gmap.canvas.draw(x,y,CHmap[2] ) places an X at coordinates (x,y) of Gmap.
Also a blank bitmap CHmap[0] is created to erase a stone.

The shifting move of a stone is done by 
procedure moveto(p,row,column : byte);
//move piece p of row to column
var x,destx,y : word;
    dx : shortInt;
    r : Trect;
begin
 movebusy := true;
 if Gpos[p,row]-column > 0 then dx := -1 else dx := 1;
 destX := (column-1)*40;
 x := (Gpos[p,row]-1)*40;
 y := (row-1)*40;
 while destX <> x do
  begin
   clearField(x,y);
   x := x + dx;
   Gmap.Canvas.Draw(x,y,CHmap[p]);
   r := rect(x-1,y,x+41,y+40);
   form1.PaintBox1.Canvas.CopyRect(r,Gmap.Canvas,r);
   delay(3);
  end;
 Gpos[p,row] := 0;
 Game[row,column] := 0;
 Gpos[p,row] := column;
 Game[row,column] := p;
end;
p = 1 if computermove, p = 2 for player move.
Rows and columns count 1..5 and 1..12
dx = 1 for right move, dx = -1 for left move.
destX is the destination column left top pixel.
Y is the row top pixelcount.
Procedure clearField[x,y] erases a 40*40 field of Gmap and restores overwritten lines.

Computer move calculation

procedure computerMove;
var d : array[1..5] of byte;
    dd : array[1..5] of byte;
    col,row,i,newColumn,sum : byte;
    OK : boolean;
begin
 row := 0;
 newColumn := 0;
 for i := 1 to rowcount do d[i] := Gpos[2,i] - Gpos[1,i] - 1;
 sum := 0;
 for i := 1 to rowcount do sum := sum xor d[i];
 if sum = 0 then
  begin
   col := 0;
   row := 0;
   for i := 1 to rowcount do
    if Gpos[2,i] > col then
     begin
      row := i;
      col  := Gpos[2,i];
     end;
   NewColumn := 1 + random(col-2);
   if NewColumn = Gpos[1,row] then inc(newColumn);
  end
  else begin
        for i := 1 to rowcount do dd[i] := d[i] xor sum;
        i := 0;
        repeat
         inc(i);
         OK := dd[i] < d[i];
        until OK or (i = rowcount);
        if OK then
         begin
          newColumn := Gpos[2,i] - dd[i] - 1;
          row := i;
         end;
       end;
 moveBusy := true;      
 delay(500);//msecs
 moveto(1,row,NewColumn);
 gamecontrol(gmCompMoved);
end;
The number of empty fields between ‘O’ and ‘X’ stones per row are stored in array d[ ].
Variable sum is the xor of d[1..rowcount].
For sum = 0 the computer generates a random move
else a move is calculated for which sum = 0;
In this case array dd[ .. ] := d[..] xor sum.
A value is choosen from dd[..] and newColumn := column – dd[..] – 1;

Game control

type TgameState = (gsIdle,gsSetUp,gsPlayer,gsComp);
     TgameMessage = (gmInit,gmNew,gmStart,gmPlayerMoved,gmCompMoved);

var gamestate : TGameState = gsIdle;
Gamestate
    - idle : no game selected or game ended
    - setUp : game selected, may reposition stones
    - Player : waiting for move of player
    - Comp : computermove in progress
Messages to procedure GameControl(gm : TGameMessage); control the game.

Message
    - Init : send when starting the game.
    - new : button is pressed
    - start : the button is pressed
    - playermoved : move finished
    - compmoved : computermove finished

The clock unit

unit clock_unit;

interface

uses windows;

procedure startClock;
function getCPUtime : single;

implementation

var t1,t2 : int64;
    frequency : single;    //millisecs

function CPUCLOCK : Int64;
asm
 RDTSC;
end;

procedure initclock;
var a : longword;
begin
 a := gettickcount;
 repeat
 until gettickcount > a;
 t1 := CPUCLOCK;
 a := a + 500;
 repeat
 until gettickcount >= a;
 t2 := CPUCLOCK;
 frequency := (t2 - t1)*0.002;
end;

procedure startClock;
begin
 t1 := CPUclock;
end;

function GetCPUtime : single;
begin
 t2 := CPUCLOCK;
 result := (t2-t1)/frequency;
end;

initialization

 initclock;

end.
The RDTSC assembler code places the 64 bit CPU clock counter in 32bit registers edx and eax.
Then wait for the update of GetTickcount which supplies the milliseconds clock about every 15 milliseconds.
Next count the CPU clock increments during 500 milliseconds.
The frequency in milliseconds is CPU cycles * 0.002.
Elapsed time is returned by
function GetCPUtime : single;

This concludes this Nim game project description.

For details please refer to the source code.

Interested in the (Delphi7) source codes?

download nim game source code
download nimresearch program
download nimresearch source code