the Pythagorean theorem

Five proofs are presented.

Introduction
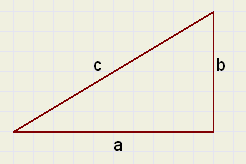
In a triangle with rectangle sides of length a en b and hypothenuse c
the equation :

    a2 + b2 = c2

is true.

This equation is known as the Pythagoras theorem.
See picture at right.

This theorem is the basis of many other theorems and calculations.
This article supplies four proofs.

Proof -1-
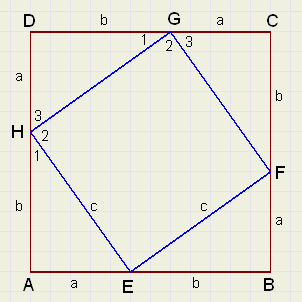We start with square ABCD.
On the sides, points E,F,G,H are placed such that AE = BF = CG = DH.
We call this distance a.
A side has length a + b.

The proof has two parts:
1. Proof that EFGH is a square.
The construction implies that triangles AEH,BFE,CGF and DHG
are congruent.
So, in any case, EFGH is a rhombus.
The length of a side we call c.
Angles (1) and (3) are 90 degrees together, so angle (2) is 90 degrees.
EFGH is a square.

2. the equation:
Let's write an area as [ ]
Look at the areas and notice that:

    [ABCD] = 4 * [AEH] + [EFGH]
    (a + b)2 = 2ab + c2
    a2 + 2ab + b2 = 2ab + c2
    a2 + b2 = c2

Proof -2-
Now we start with two unequal squares:
ABCD with a side of a
BEFG with a side of b.
Point H is on AB such, that AH = b.
Which implies that HE = a.

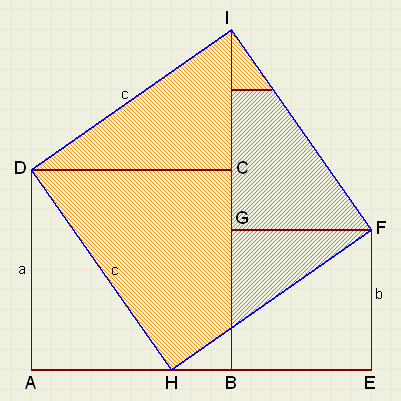We use the scissors and cut triangles ADH and HEF
placing them on sides DC and GF.

Similar to proof -1- we see, that HFID is a square.

The coloring shows:
    a2 + b2 = c2


Proof -3-
First a preamble.
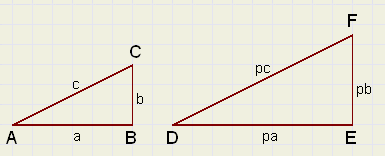
Right are pictured two triangles: ABC and DEF.
These triangles are similar:
One is an enlargement of the other, the multiplication factor is p.

Notice the similar sides: AB,DE, or AC,DF.
Similar triangles have the properties:
    - similar angles are equal
    - ratio's of similar sides are equal
Conversely: two triangles are similar if their angles are equal.

Lemma

    The areas of similar triangles have a ratio equal to the square of ratio's of similar sides
The proof unfolds: (see figure above)
Double the area of the triangles is ab and abp2.
The ratio of areas is 1 : p2 which is the ratio of similar sides, power 2.

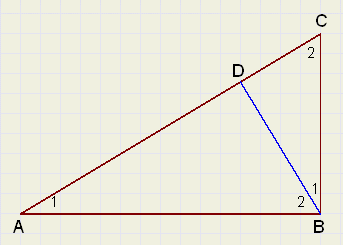Picture right has BD perpendicular to AC and AB perpendicular to BC.
There are three similar triangles: ABC, ADB and BDC.
Note the correct sequence of the angles for similarity.
Equal angles are marked equally.

With the previous knowledge we may proceed:

(call AB = a , BC = b , AC = c and notice similar hypothenuses)

We see:
    [ADB] + [BDC] = [ABC]
    [ADB] : [ABC] + [ABC] : [ABC] = 1

and because of the lemma:
    a2 : c2 + b2 : c2 = 1
    a2 + b2 = c2
Proof -4-
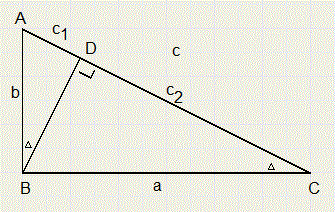Here we make use of similarity as well.

1.
    DABD ~DBCD
    c1 : b = b : c
    c1c = b2
2.
    DBCD ~DACB
    c2 : a = a : c
    c2c = a2
1. and 2. added
    a2 + b2 = c2c + c1c = (c2 + c1)c = c2

Proof -5-
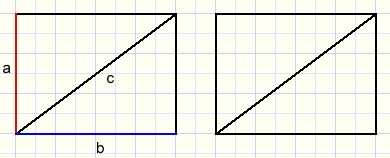Imagine two equal rectangles with sides a and b.
Cut both in half by the diagonal, which yields four equal perpendicular triangles.
The hypothenuse has length c.

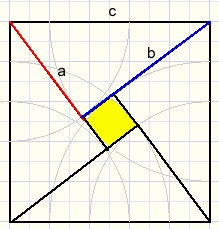Arrange the triangles as in the picture at right.

The area of the square is c2.
The original rectangles area is 2ab.
The small yellow square's area is (b-a)2.
So:
2ab + (b-a)2 = c2
2ab + b2 - 2ab + a2 = c2
a2 + b2 = c2