Stewart's theorem

Stewart's theorem is a nice extension of the Pythagorean lemma.
Please see the next picture:
The triangle has sides a,b and c.
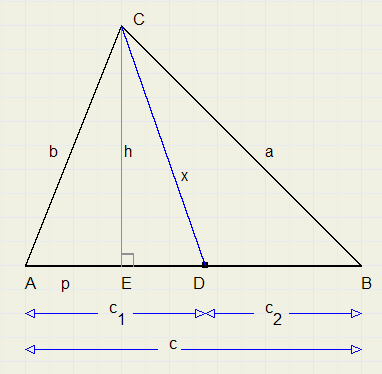
Point D splits line AB in parts c1 and c2.
AE = p, CD = x

We find a calculation for x given lengths a, b, c, c1 and c2.

Pythagoras lemma in ΔEDC
    h2 = x2 - (c1 - p)2.........1)
Pythagoras lemma in ΔAEC
    h2 = b2 - p2...................2)
...1) en ...2) combined:
    x2 - c12 + 2.c1.p - p2 = b2 - p2
    x2 = b2 + c12 - 2.c1.p......................3)
Pythagoras lemma in DEBC
    h2 = a2 - (c - p)2.................4)
...2) and ...4) combined:
    a2 - c2 +2c.p - p2 = b2 - p2
    a2 = b2 + c2 - 2c.p...............5)
...3) and ...5) combined:
    x2 = b2 + c12 - 2.c1.p ........................x c
    a2 = b2 + c2 - 2c.p.............................x c1

    c.x2 = c.b2 + c.c12 - 2.c.c1.p.........................6)
    c1.a2 = c1.b2 + c1.c2 - 2c1c.p........................7)

.........6) - .......7) yields:
    c.x2 - c1.a2 = c.b2 + c.c12 - c1.b2 - c1.c2
    c.x2 - c1.a2 = b2(c - c1) - c.c1(c - c1)
    c.x2 = c1.a2 + c2b2 - c.c1.c2
This is Stewart's theorem.

This theorem may be applied for the bisector or median of a triangle:
If x is a median:
    x2 = 1/2 a2 + 1/2 b2 - 1/4 c2
If x is bisector:
    x2 = ab - c1.c2