tree graphs programming

Programming Tree Graphs (version 5)
Delphi project

	view Delphi source code of the Tree unit.
	download Tree-exerciser program.
	download complete Delphi - 7 project

Introduction

In mathematics a graph is a picture of dots (also called node), which may be interconnected by lines.
Each dot (node) represents a situation or object.
An interconnecting line indicates a dependency between the dots or a transition.
Graph theory is about the properties of graphs.
Graphs are applied in a variety of fields such as

road maps and floor plans
electrical networks
molecules
industrial planning
combinatorics
information technology

file systems
computer games
text editing

Trees

A tree is just a type of graph.
Common properties of tree graphs are

there are no isolated nodes (each node is connected to at least one other node)
if 1 interconnecting line is removed, 2 isolated trees will result
the route from node A to B is the same as from B to A, there are no loops

Below is an example of a tree graph.
.

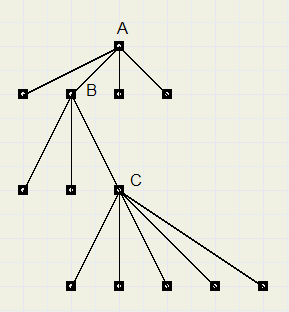
This tree could represent a file system where map A contains four files,
including map B with three files including map C containing five files.

This article is about the programming of tree graphs.
It includes creation, modifications and also undo operations.
The Delphi-7 project has three units:

All code to modify trees and undo are contained in the tree unit.
Form1, Unit1 allow testing of the tree procedures.
The data unit is only there to isolate the custom data from the tree properties.

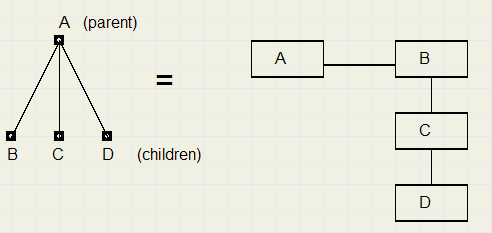
Here a graph is pictured with elements A,B,C,D.
A is called the parent. B,C,D are descendents (children) of A.
B,C,D are dependent on A in some way.

A may be a line of tekst with characters B, C and D.
Left is the math notation, right is the ICT notation known also from file systems.

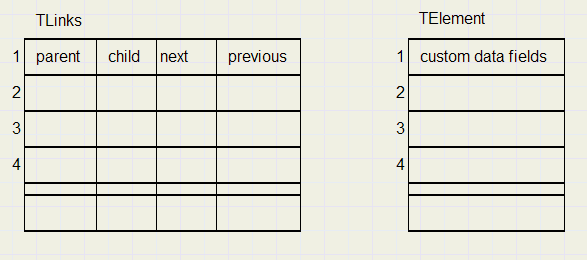
Data structures

The tree is defined by an array, where each entry represents a node .
To define connections of a node with other nodes we need the properties

Now a problem arises, because a node may have many children.
It is inconvenient to define an array per node with an entry for each child.
A better solution is to add a property next to each node to point to the next child of the parent.
To ease backward navigation between nodes, also a field previous is added to each node.

const maxelement = 50;

type TLinks  = record
                parent   : dword;
		     child    : dword;
		     next     : dword;
		     previous : dword;
		    end; 
		   
var Links : array[1..maxelement] of TLinks;

This does not include application data, which is defined in the data unit.
For the sake of demonstration this simple data is choosen:

type TElement = record
                 x : word;
                 y : word;
                end;	 
					
var Element : array[1..maxelement] of TElement;

In reality, much more data will be defined such as codes, fonts, colors, screen position etc.

Each node has a number : it's entry in both the arrays TLinks and TElement.

So, the connections of node 23 to other nodes are found in Links[23],
the data of this node is found in Element[23].

Note, that the first element in the tree is 1.
Therefore, if a node does not have a parent, child, next or previous node, this is indicated by the value 0.

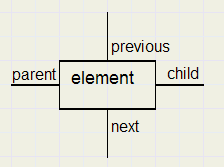
Below is pictured an element (node) and it's connections:

As an example see the tree below:

This tree drawn by the tree exerciser looks like:

Element 1 has children 2,3,4.
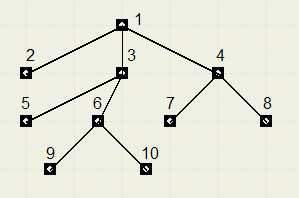
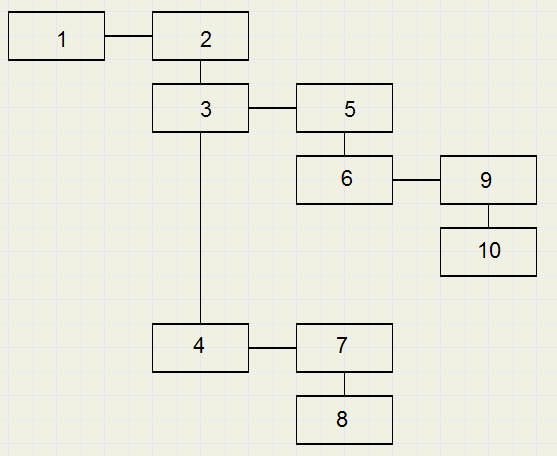
So, the parent field of nodes 2,3,4 will all be 1.
The next field of nodes 4,6,8,10 will be 0.
The previous field of nodes 1,2,5,7,9 will be 0.

Application in a math editor

Math editors are more complicated than plain text editors because of fractions, roots and other special symbols.
Below is pictured a fraction with numerator and denominator, being part of a line of text.

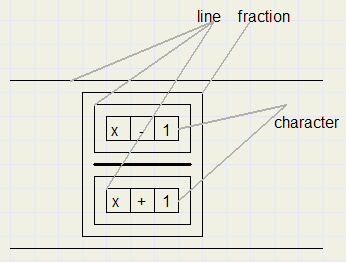
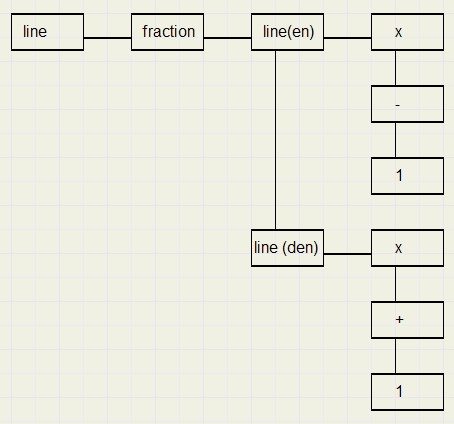
The text line is a line element with the fraction element as a child.
The numerator and denominator are lines and children of the fraction element.
The numerator line has three children: character elements with codes x, - , 1
the denominator line has children with character codes x, +, 1.

The tree structure allows for automatic alignment of text:
if the numerator length changes, the denominator position is changed to align with the numerator.

The next graph represents the fraction

Operations on Trees

Place after	place a new element after another
Place before	place a new element before another
Place Child after	place a new element as last child
Place Child before	place a new element as first child
Replace	replace an element by a new one
Pack	make element the child of a new element
UnPack	remove the parent element
Delete	remove element and it's children
Move after	move element to new position after another element
Move before	move element to a new position before another element
Move Child after	move element after last child of another element
Move Child before	move element before first child of nother element
undo	cancel the last operation

Element status

The status of an element is stored in bit positions 24..31 of the parent field.

type  TElementStatus = (esFree,esActive,esDeleted,esReplaced,esUnpacked);

mark

Marking an element is not part of the tree operations, but only a function of the exerciser.
The links of the marked element are displayed at the left bottom of the screen.

Place after, Place before

procedure PlaceA(del,sel : dword);//place free element sel after del
procedure PlaceB(del,sel : dword);//place free element sel before del

This operation provides for adding elements: typing text, inserting tables, parenthesis, fractions
or the insertion of text lines on a page.

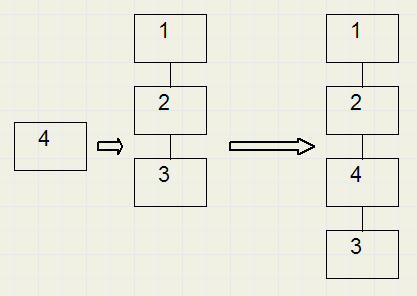
Place after: Element 4 is inserted after element 2.
Place before: Element 4 is placed before element 3.

Place Child after, place Child before

 procedure PlaceChildA(del,sel : dword);//place free element sel as last child of del
 procedure PlaceChildB(del,sel : dword);//place free element sel as first child of del

This operation adds a new child to an element.
The child's position is either as the first or the last.
The operations are identical if the element has no children yet.
Element 5 is inserted as the first child of element 1.
Element 5 is inserted as the last child of element 1.

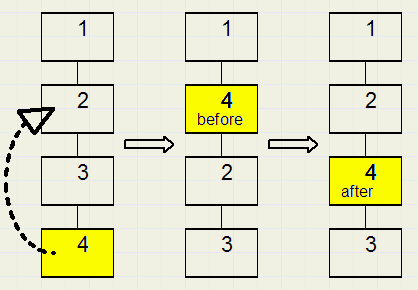
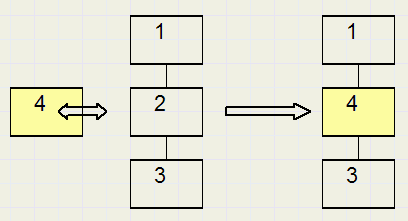
Move element after , before

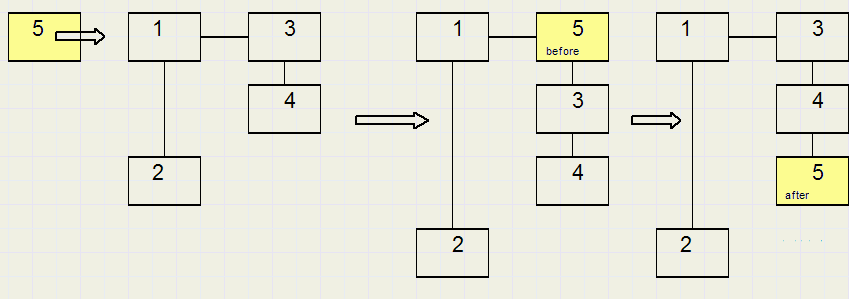
procedure moveElA(del,sel : dword);//move active element sel after del
procedure moveElB(del,sel : dword);//move active element sel after del

This operation removes element sel from the tree and inserts it after ( before) element del.

Replace

procedure ReplaceEL(del,sel : dword);//replace element del by sel
//sel must be free element
//del is part of tree

Replace an element by a new element. Element 2 is replaced by element 4.

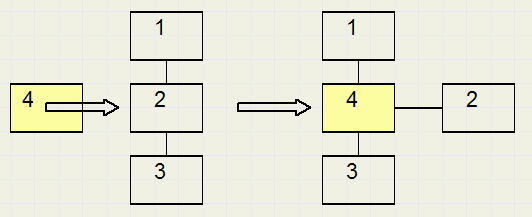
Pack

procedure packEl(del,sel : dword);//free element sel becomes parent of del

Make an element the child of a new element.
Element 2 becomes the child of element 4

UnPack

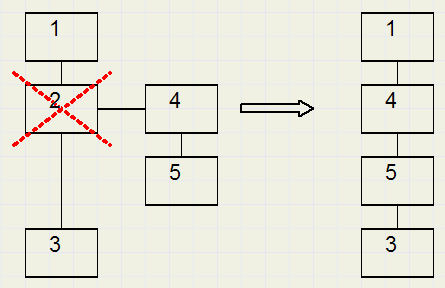
procedure unpackEl(sel : dword);//remove active element sel, children not deleted

Remove the parent of an element.
Element 2 as parent of elements 4,5 is removed.

Delete

procedure deleteEL(del : dword);//delete element del, do not delete children

The selected element is removed from the tree, together with it's children.

Using the exerciser

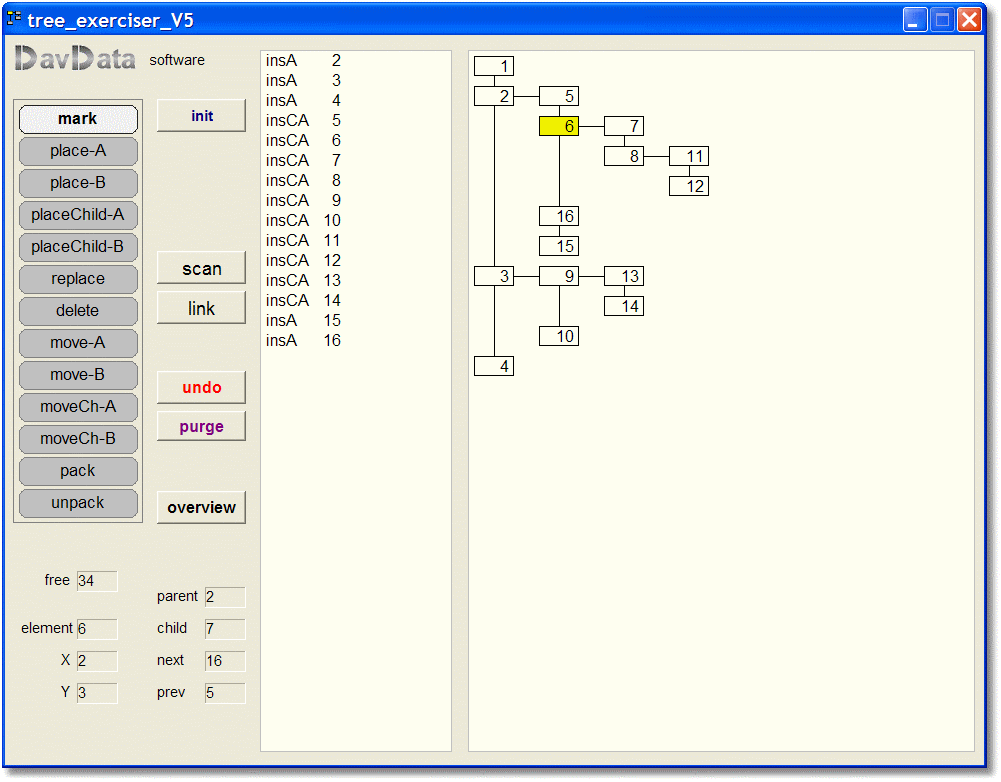
For operations PlaceA, PlaceB, PlaceChildA, PlaceChildB, Replace, Pack, UnPack, Delete:

Place mousepointer over element and click. For operations moveA, moveB, moveChildA, moveChildB:

The Undo system

Each operation is stored in a stack structure with entries:

const maxUndo = 25;
....
type TLinkType      = (ltNone,ltParent,ltChild,ltNext,ltPrevious);
     TELaction      = (eaPlaceA,eaPlaceB,eaPlaceChildA,eaPlaceChildB,eaReplace,
                       eaDelete,eaMoveA,eaMoveB,eaMoveChildA,eaMoveChildB,
                       eaPack,eaUnpack,eaUndo,eaNone);
     TEditAction = record
                    action  : TELaction;
                    elmnt   : dword;     //element
                    linkEl  : dword;     //link element
                    linktype: TLinkType;
                    cc      : dword;     //child count
                    bwlink  : boolean;   //backward link
                   end;
.........
var startflag,linkflag : boolean;
    UndoStack : array[1..maxundo] of TEditAction;

Fields are:

This information enables the reverse of previous operations.
Constant maxUndo is the maximum number of operations saved to be backed up.

To Undo the last operation

procedure UndoAction;

To clear the Undo stack, removing all stored Undo data:

procedure purgeUndoStack;

To link the next operation(s), Undoing them together at a later time:

procedure startLinking;

To stop linking operations, undoing them separately later:

procedure stoplinking;

Getting the saved Undo data in the stack:

function getstackdata(n : word) : TEditAction;

Linking

In reality, an edit action may involve several basic tree operations.
An Undo operation has to include all operations that belong together.
Therefore the bwlink flag may be set, to link an entry in the Undo Stack to the previous entry.

procedure startlinking sets the startflag and clears the linkflag.
procedure registerAction pushes the undo information to the stack and than copies the startflag in the linkflag.
The next operations are now registered with bwlink := linkflag, so are linked to the earlier operation.
procedure stoplinking clears the startflag and the linkflag.

Destroying elements

Deleted or replaced elements are saved with their links and properties, because an undo operation
may make them active again.
There is no public procedure to free (destroy) an element directly.
However, if the UndoStack is full and another edit operation takes pace on the tree,
then the stack has to shift up which purges entry 1.
If this entry stored a deleted, replaced or unpacked element, it is impossible to put
this element into action again because it is outside the range of Undo.
Therefore this element is destroyed, giving it the free status so it may be used by future operations.

Programming

Initialization

At the beginning, the tree has to be initialized:

procedure initTree;

This clears all links and sets Links[1] to active.

Links[1] may not be deleted, it is always the start (top) of the tree.

In the data unit:

procedure initTreeData;

Clears all data fields in array Element[ ]

New elements added to the tree must be free.
To get the number of a free element:

function getFreeEl(var el : dword) : boolean;//return free element number el
//return true if Ok, false if out of elements

Navigating

function ParentEl(var nel : dword) : boolean;
function ChildEl(var nel : dword) : boolean;
function NextEl(var nel : dword) : boolean;
function previousEl(var nel : dword) : boolean;

The parent, child, next or previous element of nel is returned.
If no such element is present, nel is not changed and a false result is generated.

function ScanElement(var elmnt : dword; lt : TLinkType) : TLinktype;

From element elmnt the next element is returned depending on the link type lt.
The purpose of this function is to step through the elements in a systematical way:

The scanelement function is used to paint the tree.
Successive calls to this function first addresses all children, then the next elements.
The elements are adressed twice: during the forward and during backward scan.
The protected procedure destroyELch uses the scanelement function as well
to destroy an Element together with it's children

Status

getting all links of an element:

function GetElLinks(n : dword) : TElLinks;

getting the status of an element:

function getELStatus(el : dword) : TElementStatus;

Getting the number of children of an element:

function getChildCount(del : dword) : dword;

getting the last child of an element:

function getLastChild(del : dword) : dword; //return 0 if no child

Getting the tree's number of free elements, the last assigned element and the number of stored Undo actions:

function getTreeStatistics : TTreestats;//return tree statistics

Undo

   procedure UndoAction;

Undos the last action.
Added elements are removed from the tree and destroyd (= given the free status).
Deleted and replaced elements are restored.

To clear the complete Undo stack, making further Undos impossible:

   procedure purgeUndoStack;

This is also a way to destroy all deleted or replaced elements, generating new free elements to be used.

This concludes the tree-graph description.
For more details please refer to the source code.