regelmatige veelvlakken

Regelmatige Veelvlakken

Inleiding
Een regelmatig veelvlak is een ruimtelijke vorm bestaande uit platte vlakken,
die allemaal dezelfde vorm hebben en waarvan alle ribben gelijk zijn.
De bekendste regelmatige veelvlakken zijn de (vierzijdige) piramide en de kubus.
Zie de figuur 1. hieronder.

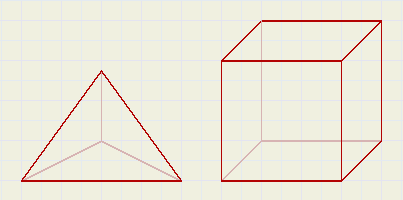fig. 1

We vragen ons af, of er nog meer regelmatige veelvlakken bestaan.
In dit artikel onderzoeken we dat en vinden het antwoord.
Hierbij is nodig een stelling van de wiskundige Euler (1707 - 1783), over
vlakken, zijden en hoekpunten.

De stelling van Euler
Bekijk de figuren 2.1 .. 2.4 hieronder:

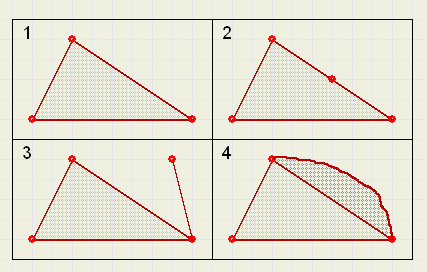fig. 2

In fig. 2.1 zie je een rechthoek met daarin getekend een driehoek.
De rechthoek is zodoende verdeeld in 2 vlakken : het deel buiten -
en het deel binnen de driehoek.
Verder tel je 3 ribben (lijnen) en 3 (hoek) punten.

Nu zetten we in fig. 2.1 een nieuw punt op één van de ribben : zie fig. 2.2.
Hierdoor tellen we nog steeds 2 vlakken, maar nu zijn er 4 lijnen en ook 4 hoekpunten.

Een nieuw punt had ook buiten de driehoek gezet kunnen worden, zie fig. 2.3.
Het aantal vlakken neemt dan niet toe en er zijn één lijn en één punt bijgekomen.

Figuur 2.4 is uit 2.1 ontstaan door alleen een lijn toe te voegen en geen punten.
Het aantal vlakken neemt zo met één toe.

Noemen we het aantal vlakken V, de ribben R en de (hoek) punten H, dan leiden we uit
het voorgaande af:

V = R - H + 2 Deze stelling is door de wiskundige Euler bedacht.

opmerking:
Losse lijnen zijn niet toegestaan.
Elke lijn begint en eindigt in een punt.

Projecteren
In gedachten brengen we binnen een veelvlak een lichtbron aan die de ribben
projecteert op een bol om het veelvlak.
Op die projectie geldt de wet van Euler.
De variabelen zijn hierin het aantal vlakken, ribben en hoekpunten.
Als twee variabelen bekend zijn, dan is de derde dus eenvoudig te berekenen.

In het geval van de vierzijdige piramide:

Nadere voorwaarden
We bekijken de losse vlakken van een kubus:

fig. 3

Als we vanuit elk (los) vlak het aantal ribben of hoeken tellen, dan vinden we er 6 * 4 = 24

Algemeen:
Als er V vlakken zijn en een vlak heeft n hoeken (dus ook n ribben),
dan tellen we n*V ribben en hoeken.
Bedenkend, dat elke ribbe in twee vlakken ligt en dus dubbel is geteld, moet gelden:

R =

n V

Vanuit de V vlakken samen zijn nV hoeken geteld.
Stel nu, dat elk hoekpunt in m vlakken ligt.
Dan is elke hoek m keer geteld en er zijn dus

H =

n V

hoeken.

Nu .....1) en .............2) invullen in de formule van Euler ( V = R - H + 2):

V =

n V

−

n V

+ 2

V =

4 m

2 m − n (m − 2)

De voorwaarden bij de vergelijking hierboven zijn:

aangezien er voor een ruimtelijke vorm minstens drie vlakken en drie ribben
in een hoekpunt moeten samenkomen.

V moet positief zijn, zodat in formule ...........3)

2 m

m − 2

Uit het voorgaande volgt ook:

2 m

m − 2

> 3

De voorwaarden voor m samengevat:

m (het aantal vlakken waarin een hoekpunt ligt) kan alleen de waarden 3,4,5 aannemen.
Uitgaande van deze waarden zoeken we de waarden van n (ribben per vlak) en van V (aantal vlakken).

Door een waarde te kiezen van m vereenvoudigt formule ...............3)

Het geval m = 3 (3 vlakken per hoekpunt)
Formule .........3) wordt:

V =

6 − n

Het geval m = 4(4 vlakken per hoekpunt)
Formule .........3) wordt:

V =

4 − n

Het geval m = 5(5 vlakken per hoekpunt)
Formule .........3) wordt:

V =

10 − 3 n

Samenvatting
Voor elk paar waarden van m en n zijn V , R en H te berekenen met de formules ...1) t/m ....3)

vlakken	ribben	hoekpunten	afbeelding
4	6	4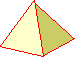
6	12	8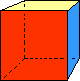
8	12	6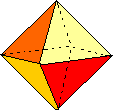
12	30	20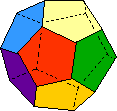
20	30	12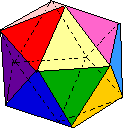
fig. 4