

 |
Rekenen met Breuken |  |
 |
Delen is het omgekeerde van vermenigvuldigen.
Als we een getal door 5 delen en de uitkomst weer met 5 vermenigvuldigen,
dan is het antwoord gelijk aan het oorspronkelijke getal.
-
15 : 5 * 5 = 15
-
1 : 5 * 5 = 1
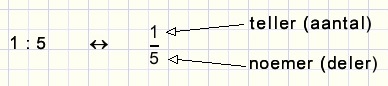
Definities
| de betekenis van | is: er zijn 5 van die stukjes nodig om weer één hele te maken. |
Gehele getallen schrijven als breuk
Elk geheel getal kan als breuk worden geschreven, zo is:

de + regel
We bezoeken een houtzagerij, waar planken van lengte 1 in 5 gelijke delen worden gezaagd.
(speciale zagen: er treden geen verliezen op), zie plaatje hieronder:
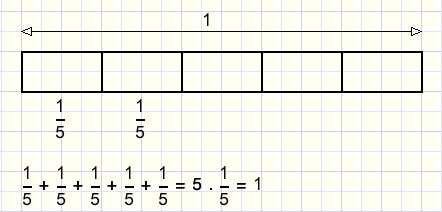
Er kunnen ook 2 of meer planken tegelijk worden gezaagd:
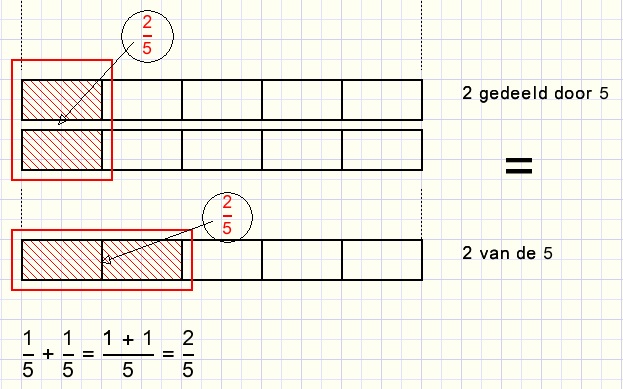
Door ook 3, 4, 5, 6 .... planken tegelijk in gelijke delen te zagen, zien we de + regel voor breuken:
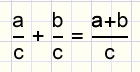
-
breuken met gelijke noemers tel je op door de tellers op te tellen en de noemer gelijk te laten.
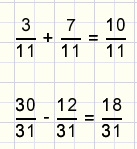
de * regel
De uitkomst van een vermenigvuldiging vatten we even op als de oppervlakte van een rechthoek:
immers: lengte * breedte = oppervlakte.
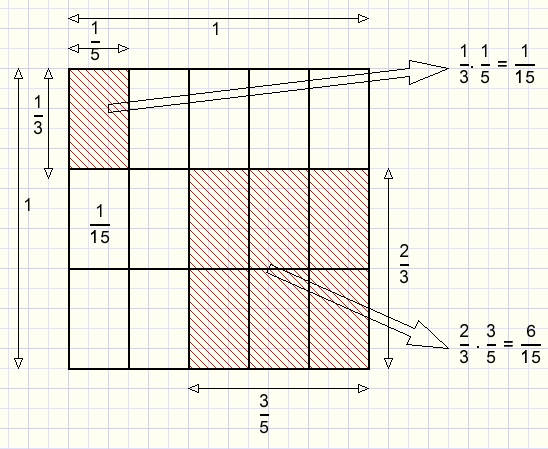
De gehele oppervlakte van de plaat is gelijk aan 1.
Door de plaat vertikaal in 3 en horizontaal in 5 delen te zagen, ontstaan 3 * 5 = 15 delen.
In formule:
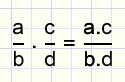
voorbeelden:

De + en de * regel zijn de basisregels voor het rekenen met breuken.
Alle andere regels kunnen eenvoudig van deze twee basisregels worden afgeleid.
Vereenvoudigen
Een een getal, dus ook een breuk, verandert niet als we die met 1 vermenigvuldigen.
(1 heet het "neutrale" getal voor vermenigvuldigen).

In woorden:
- Een breuk verandert niet als
1. teller en noemer met hetzelfde getal worden vermenigvuldigd of
2. teller en noemer door hetzelfde getal worden gedeeld.
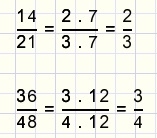
Optellen bij ongelijke noemers
De noemers moeten eerst gelijk worden gemaakt door per breuk met een geschikt getal te vermenigvuldigen.
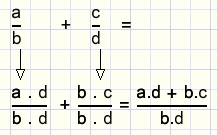
De nieuwe noemer wordt bd.
Als b en d gemeenschappelijke factoren bevatten, dan volstaat een kleinere noemer, nl. KGV(b,d).
Zie hiervoor artikel Factoren, GGD, KGV
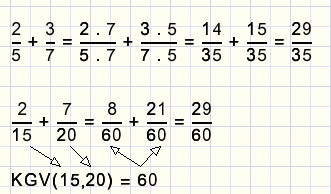
Voorbeelden:
Schrijven als breuk
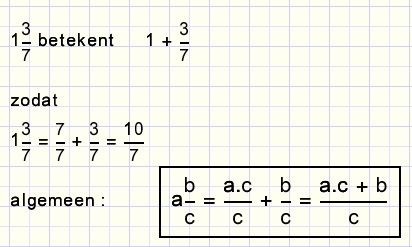
de "helen" eruit halen
Een breuk is groter dan 1, als de teller groter is dan de noemer.
In dat geval kunnen de "helen" worden afgesplitst door een veelvoud van de noemer
van de teller af te trekken.
Voorbeeld:
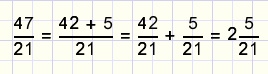
Omgekeerden
De "omgekeerde" van een breuk ontstaat als teller en noemer van plaats verwisselen.
Het product van een breuk met zijn omgekeerde levert altijd 1 op:
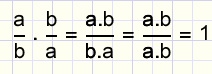
Delen door een breuk
Door zowel teller als noemer te vermenigvuldigen met de omgekeerde noemer ontstaat:
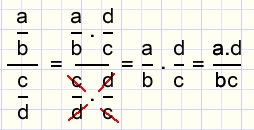
- delen door een breuk is hetzelfde als vermenigvuldigen met de omgekeerde

Procenten
Procent betekent "deel van 100".
Als de noemer van een breuk 100 is dan is de teller het percentage.
Om een breuk naar een percentage om te rekenen moet de noemer dus 100 worden gemaakt.
Algemeen:

Voorbeeld:
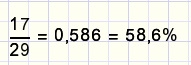
Toepassing
Zie figuur hieronder met een (water)leidingnet.
De breuken geven aan, hoe het water zich bij elke splitsing verdeelt.
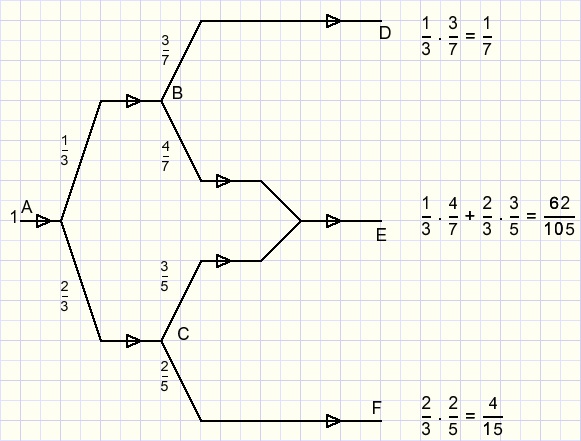
Opmerking: achter elkaar : vermenigvuldigen, samenvoegen : optellen.
De aantallen bij D,E,F moeten opgeteld 1 opleveren.


