Meetkunde problemen en oplossing met rotatie

Meetkundeproblemen waarvan de oplossing rotatie vereist zijn doorgaans lastig.
In dit artikel geef ik drie voorbeelden.

Probleem 1




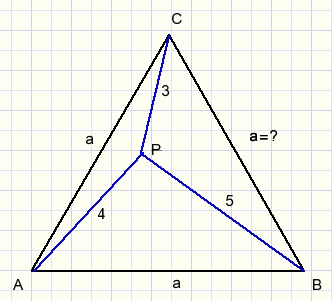
Gegeven is de een gelijkzijdige driehoek ABC met daarbinnen punt P.
Er geldt:
    PC = 3
    PA = 4
    PB = 5
Gevraagd: de lengte a van de zijden van de driehoek.

De oplossing komt in zicht door 60 graden rotatie rechtsom van driehoek BPC om het punt B.
Punt P wordt na rotatie P', C' = A.
Driehoek PP'B is gelijkzijdig, zodat PP'=5.
Driehoek PC'P' is wegens de zijden 3,4,5 (Pythagoras drietal) rechthoekig.
Na rotatie over 60 graden staan zijden AP en AP' loodrecht op elkaar.
Vóór rotatie was hun hoek dus 90 + 60 = 150 graden (LAPC)



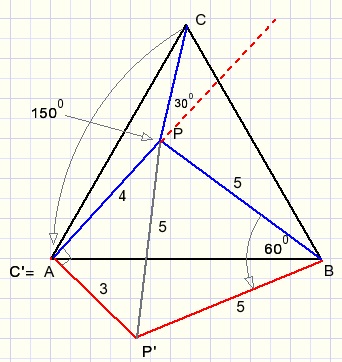
Toepassing van de cosinus regel in driehoek APC geeft zijde a:
    a2 = 32 + 42 - 2.3.4.cos(1500)
    a2 = 25 - 24.(-0,866)
    a = 6,766
In DIT artikel verkrijg ik hetzelfde rsultaat met een Delphi programma
waarin a numeriek wordt berekend met een benaderingsmethode.

Probleem 2




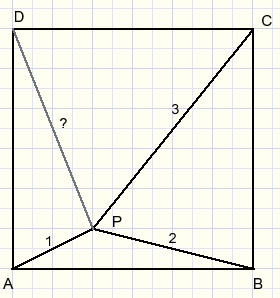
Gegeven is vierkant ABCD met daarbinnen punt P.
Er geldt:
    AP = 1
    BP = 2
    CP = 3
Onbekend is de lengte van de zijden van het vierkant.
Gevraagd: de afstand DP.

Voor de oplossing van dit probleem zijn twee rotaties nodig.
1.
Neem C als rotatie middelpunt en draai driehoek CPB 90 graden rechtsom.
2.
Neem A als rotatie middelpunt en draai driehoek ABP 90 graden linksom.



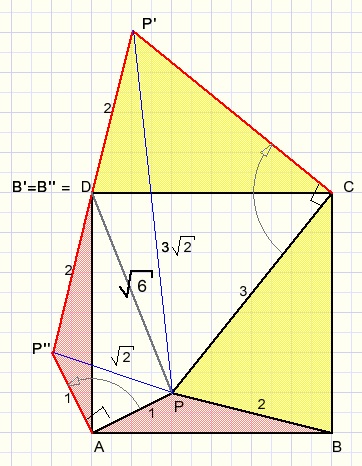
In de figuur hierboven is P'DP'' een rechte lijn omdat P'D een draaiing 90 graden rechtsom is van BP
en P''D een draaing 90 graden linksom is van BP.

Driehoek PCP' is een gelijkbenige rechthoekige driehoek zodat (Pythagoras) PP' is te berekenen.
Het zelfde geldt voor driehoek APP'' en zijde PP''.
In driehoek P''PP' is PD zwaartelijn en de lengtes van de zijden zijn bekend.
Met de zwaartelijn formule kan nu PD worden berekend.
Opmerking:
de zwaartelijn formule is een speciaal geval van de stelling van Stewart zie [HIER]



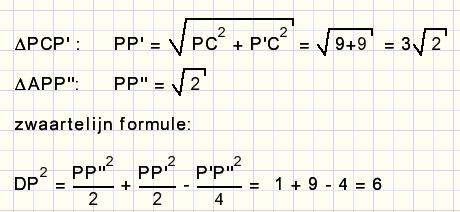
Tenslotte:
Welke lengte heeft een zijde van het vierkant?
Aanwijzing :
1. gebruik de cosinusregel of
2. bedenk dat 5 hoek APCP'P'' dezelfde oppervlakte heeft als vierkant ABCD.

Probleem 3




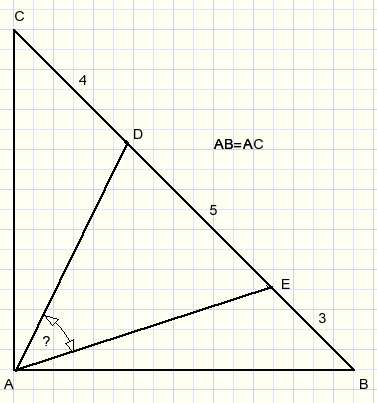
Gegeven is rechthoekige en gelijkbenige driehoek ABC (AB = AC).
Gevraag is LDAE.

De 3,4,5 lengtes herinneren ons aan de stelling van Pythagoras.
Roteer driehoek ABC in de draairichting van de klok met 90 graden.
A is het centrum van de rotatie.
zodat:
    C wordt C'= B
    D --> D'
    E --> E'
zie de figuur hieronder:



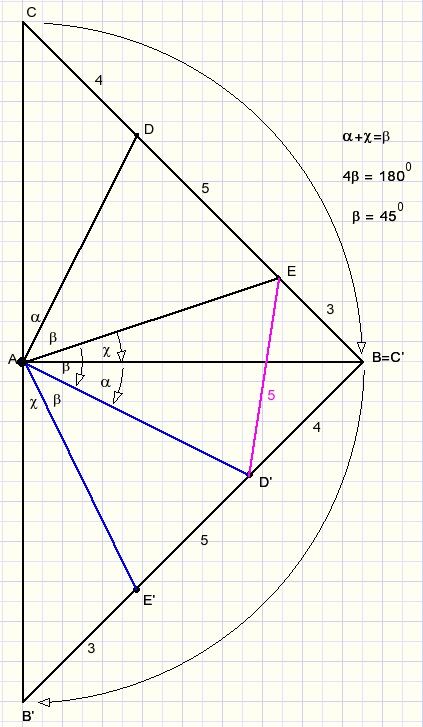
Omdat AD'= AD en D'E = 5 (32+42=52) zijn driehoeken ADE en AD'E congruent.
Merk ook op dat:
    LCAD = LC'AD'
    LEAB = LE'AB'