cursus goniometrie (5)

Inhoud

gonio1Inleiding. sin, cos, tan
gonio2grafieken en trillingen
gonio3sinusregel en cosinusregel
gonio4formules
gonio5vergelijkingen

Inleiding

Dit laatste deel van de cursus goniometrie gaat over het oplossen van vergelijkingen.

sin(x) = sin(a)

De oplossing van deze vergelijking is
    x = a + k.360
    of
    x = 180 - a + k.360

voorbeeld (1)

sin(x) = 0,5

    bgsin(0,5) = 30
    sin(x) = sin(30)
    x = 30 + k.360
    of
    x = 150 + k.360

voorbeeld (2)

4sin(3x - 15) = 1

    sin(3x - 15) = 0,25
    bgsin(0,25) = 15 ..................(beetje afgerond)
    sin(3x - 15) = sin(15)
    3x - 15 = 15 + k.360
    x = 10 + k.120
    of
    3x - 15 = 165 + k.360
    x = 60 + k.120

cos(x) = cos(a)

De oplossing van deze vergelijking is
    x = a + k.360
    of
    x = - a + k.360

voorbeeld (3)

2sin2(x) + 3cos(x) = 0

    vervang sin2(x) door 1 - cos2(x) .............zodat........
    2 - 2 cos2(x) + 3cos(x) = 0
    2cos2(x) -3cos(x) - 2 = 0
    stel cos(x) = t, .............zodat..........
    2t2 - 3t - 2 = 0...............ontbinden in factoren:
    (2t + 1)(t - 2 ) = 0
    t - 2 = 0..................kan niet, want cos(x) is minimaal -1
    of
    2t + 1 = 0
    t = -0,5
    cos(x) = -0,5 = cos(120)
    x = 120 + k.360
    of
    x = -120 + k.360

tan(x) = tan(a)

De oplossing van deze vergelijking is
    x = a + k.180

voorbeeld (4)

sin2(x) + 2sin(x)cos(x) - cos2(x) = 0

    2sin(x)cos(x) - (cos2(x) - sin2(x)) = 0
    sin(2x) - cos(2x) = 0.................delen door cos(2x).............
    tan(2x) - 1 = 0
    tan(2x) = 1 = tan(45)
    2x = 45 + k.180
    x = 22,5 + k.90

a.sin(x) + b.cos(x) = c

Er zijn verschillende manieren om een vergelijking van dit type op te lossen.

Aanpak 1.

We grijpen terug op de grafieken van sinus en cosinus: ronddraaiende punten op een cirkel.
Maar in plaats van een punt gebruiken we een vector (gericht lijnstuk), zie plaatje:
vector MA = a.sin(x) getekend voor x = 0.
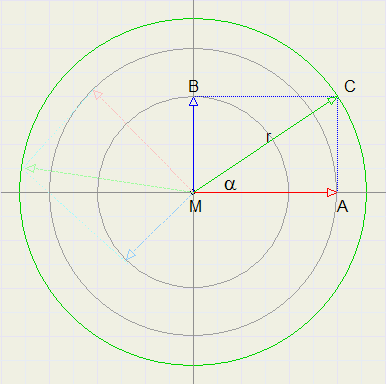
Als x verandert, dat draait MA om punt M.
De waarde van a.sin(x) is de afstand van A tot de horizontale as.

b.cos(x) is te schrijven als b.sin(x + 90), een sinusfunctie met amplitude b, die 90 graden op sin(x) voorloopt.
Op moment x = 0 stelt vector MB b.sin(x+90) voor, waarbij de afstand van B tot de horizontale as de grootte
weergeeft van b.sin(x+90).
t = MC =MA + MB is dan de vector optelling en stelt de waarde voor: ........a.sin(x) + b.cos(x)

a.sin(x) + b.cos(x) is dus te vervangen door
    r.sin(x + a)
Nu moeten r en a nog worden bepaald:
    MA = a, MB = b, .........zodat
    r = MC =
    \a 2 + b 2
    a = bgtan(
    b
    a
     )
Nu bevinden we ons weer in bekend vaarwater:
    r.sin(x + a) = c
    sin(x + a) = c/r
    sin(x + a) = sin(bgsin(c/r))
    x + a = bgsin(c/r) + k.360..................enzovoorts

Voorbeeld 5

5sin(x) - 12cos(x) = 6

    r =
    \5 2 + 12 2
     = 13
    a = bgtan(-12/5) = -67,38
    13sin(x - 67,38) = 6
    sin(x - 67,38) = 0,4615.... = sin(27,49)
    x - 67,38 = 27,49 + k.360
    x = 95 + k.360...............(beetje afgerond)
    of
    x - 67,38 = 180 - 27,49+ k.360
    x = 220 + k.360............(beetje afgerond)

Let op: - cos(x) = betekent een spiegeling van MB om de horizontale as, hoek a is dan negatief


Aanpak 2.

a.sin(x) + b.cos(x) = c
Bovenstaande vergelijking wordt herleid tot de vorm
    sin(x).cos(a) + cos(x)sin(a) = p.............zodat
    sin(x + a) = p
Truuk: vermenigvuldig met k
    ka.sin(x) + kb.cos(x) = kc
bepaal nu de waarde van k zodanig, dat geldt
    ka = cos(a)
    kb = sin(a)
Omdat sin2a + cos2a = 1 geldt....
    k2a2 + k2b2 = 1
    k =
    1
    \a 2 + b 2
     ........................(vergeet de negatieve wortel van k)
    zodat:
    sin(x + a) = kc,
    waarbij a = bgsin(kb).....................enzovoorts
Eigenlijk doen we hier hetzelfde als bij aanpak 1.

Omzetten naar een algebraïsche vergelijking

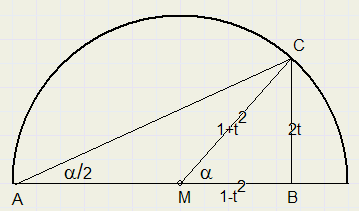
In het plaatje hierboven is MC de straal van een halve cirkelboog
    MB = 1-t2
    BC = 2t
    MC = 1+t2
Ga na, dat in driehoek MBC de stelling van Pythagoras klopt.

Uit het plaatje is verder af te lezen dat
    tan(a/2) = t
    sin(a) =
    2 t
    1 + t 2
    cos(a) =
    1 − t 2
    1 + t 2
    tan(a) =
    2 t
    1 − t 2

Aanpak 3.

a.sin(x) + b.cos(x) = c .............kan dus herschreven worden als
    2 a t
    1 + t 2
     + 
    b − b t 2
    1 + t 2
     = c
    wat omgewerkt kan worden tot
    2at + b - bt2 = c + ct2
    (c+b)t2 - 2at + (c-b) = 0
Nu staat er een kwadratische vergelijking, waaruit met de ABC formule t = tan(x/2) is te berekenen,
waaruit weer x is te berekenen.
Aan de discriminant in de ABC formule is meteen het aantal oplossingen te zien.

Voorbeeld 6.

4sin(x) - 5cos(x) = 6

    8 t
    1 + t 2
     − 
    5 − 5 t 2
    1 + t 2
     = 6
    t2 - 8t + 11 = 0.......................ABC formule.............
    t1 = 6,236
    a/2 = bgtan(6,236) + k.180 = 80,88 + k.180
    a = 162 + k.360
    of
    t2 = 1,76
    a/2 = bgtan(1,76) + k.180 = 60,395 + k.180
    a = 120,8 + k.360
Hiermee besluit ik deze korte, maar toch volledige cursus goniometrie.

Opgaven

los x op uit de volgende vergelijkingen:
1.
a.............10sin(2x - 60) = 5
b..............2tan(5x + 30) = 2

2.
a.....sin(x) = cos(x)
b.....sin(x) = - cos(x)

3.
a.......sin(3x) = sin(x)
b.......2sin2(x) - sin(x) = 0

4.
a.........tan(x) = 2sin(x)
b.........2tan(x) = sin(2x)

5.
a.........4sin2(x) + 4cos(x) - 5 = 0
b.........8cos4(x) + 6sin2(x) - 5 = 0

6.
a..........sin(x) + cos(x) = 1
b..........3sin(x) + 4cos(x) = 5

7.
a..........8cos(x) + 15sin(x) = 17
b..........4sin(x).cos(x) - 2cos2(x) = 1

8.
a...........sin(x + 18) + sin(x - 18) = 1
b...........sin(x) + cos(x) + tan(x) + 1 = 0

9.
a...........tan(2x) + tan(3x) = 3tan(x)
b...........sin(x) - cos(x) = 0,5sin(x).cos(x)

10.
a.............9sin2(x) + 2cos(3x).(2sin(3x) + cos(3x)) = 2 + 24sin4(x) - 16sin6(x)
b.............
cos x
cos (2 x)
 + 
5 ·  sin x
sin (2 x)
 = 0

succes!


Antwoorden.
De oplossing van een vergelijking is altijd te vinden door de formules links en rechts van het = teken
te plotten en het snijpunt af te lezen.
Neem de vergelijking sin(x) = cos(x):
Plot de grafieken van
1. y = sin(x)
2. y = cos(x)
en lees x af voor de snijpunten.

Gebruik het grafiekenprogramma Graphics-Explorer
Stel in vervangen en graden
Stel de horizontale schaal in op ca. 10..30 graden per schaaldeel.

1.
a.
10sin(2x-60) = 5
sin(2x-60) = sin(30)
2x-60 = 30 + k360
x=45 + k180		 2x-60 = 150 + k360
x = 105+ k180

b.
2tan(5x+30) = 2
tan(5x+30) = tan(45)
5x + 30 = 45 + k180
x = 3 + k36

2.
a.
sin(x) = cos(x) = sin(90-x)
x = 90 - x + k360
x = 45 + k180
b.
sin(x) = - cos(x) = - sin(90 - x) = sin(x - 90)
x = 180 - (x- 90) + k360
x = 135 + k180

3.
a.
sin(3x) = sin(x)
3x = x + k360
x = k180		 3x = 180 - x + k360
x = 45 + k90

b.
2sin2(x) - sin(x) = 0
sin(x).(2sin(x) - 1) = 0
sin(x) = 0 = sin(0)
x = 0 + k360		 x = 180 + k360
x = 45 + k90		 2sin(x) - 1 = 0
sin(x) = sin(30)
x = 30 + k360
of
x = 150 + k360


4.
a.
tan(x) = 2sin(x)
sin(x) / cos(x) = 2sin(x)
sin(x) .(2 - 1/cos(x)) = 0
sin(x) = 0
x = k180		 2 - 1/cos(x) = 0
cos(x) = 1/2 = cos(60)
x = 60 + k360
of
x = -60 + k360

b.
2tan(x) = sin(2x)
2sin(x) / cos(x) = 2sin(x)cos(x)
sin(x) .(1 / cos(x) - cos(x)) = 0
sin(x) = 0 = sin(0)
x = 0 + k180		 cos2(x) = 1
cos(x) = 1
x = k360		 cos(x) = -1
x = 180 + k360


5.
a.
4sin2(x) + 4cos(x) - 5 = 0
4(1 - cos2(x) + 4cos(x) - 5 = 0
cos2(x) - cos(x) + 1/4 = 0
(cos(x) - 1/2)2 = 0
cos(x) = cos(60)
x = 60 + k360
of
x = -60 + k360
b.
8cos4(x) + 6sin2(x) - 5 = 0
stel cos2(x) = p...............
8p2 -6p + 1= 0
p = 1/2
cos(x) = + 1/2W(2)
x = 45 + k360....of..........x = -45 + k360
of
cos(x) = -1/2W(2)
x = 135 + k360.........of...........x = -135 + k360 		p = 1/4
cos(x) = 1/2
x = 60 + k360.......of ............x = -60 + k360 of
cos(x) = -1/2
x = 120 + k360............of..............x = -120 + k360


6.
a.
sin(x) + cos(x) = 1
W(2)sin(x + 45) = 1 sin(x + 45) = 1/2 . W(2) = sin(45)
x = k360
of
x + 45 = 180 - 45 + k360
x = 90 + k360
b.
3sin(x) + 4cos(x) = 5
5sin(x + 53) = 5
x = 37 + k360
of
x = 153 + k360

7.
a.
15sin(x) + 8cos(x) = 17
30 t
1 + t 2
 + 
8 − 8 t 2
1 + t 2
 = 17
25 t 2 − 30 t + 9 = 0
(5 t − 3) 2 = 0
t = 3/5..............sin(x) = 15/17
x = 62 + k360
b.
4sin(x)cos(x) - 2cos2(x) = 1
2sin(2x) - (1 + 1 - 2sin2(x)) = 1
2sin(2x) - cos(2x) = 2
W(5).sin(2x-26,6) = 2
2x-26,6 = 63,4
x = 45 + k180 		2x - 26,6 = 180 - 63,4 + k360
x = 71,6+ k180

8.
a.
sin(x+18) + sin(x-18) = 1
sin(x)cos(18) + cos(x) sin(18) + sin(x)cos(-18) + cos(x) sin(x-18) = 1
2sin(x)cos(18) = 1
sin(x) = sin(31,7)
x= 31,7 + k360...........of...............x = 148,3 + k360
b.
sin(x) + cos(x) + tan(x) + 1 = 0
2 t
1 + t 2
 + 
1 − t 2
1 + t 2
 + 
2 t
1 − t 2
 + 1 = 0
t2-2t -1 = 0
t = 1 + W(2)
t = 2,4142 = tan(x/2)
x = 135 + k360 		t = 1 - W(2) = -0,4142
x = -45 + k360

Opmerking: de oplossing x = k180 komt hier niet tevoorschijn. Tekortkoming van de T substitutie?

9.
a.
tan(2x) + tan(3x) = 3tan(x)
schrijf als tan(x), stel dan: tan2(x) = p, dat levert:
2
p
 + 
3 − p
1 − 3 p
 = 3
delen door tan(x), dus oplossing is
tan(x) = 0.............x = k180.
8p2 + p - 4 = 0
p = 0,647....
tan(x) = +- 0,804
x = - 38,8 + k180..............of...........x = 38,8 + k180
b.
sin(x) - cos(x) = 0,5sin(x).cos(x)
Het rechterlid doet denken aan het dubbelproduct van (sin(x) + cos(x))2
Dus vooraf eerst eens onderzoeken:
(sin(x) - cos(x))2 = sin2(x) + cos2(x) - 2sin(x).cos(x) = 1 - 2sin(x).cos(x)
stellen we sin(x) - cos(x) = y, dan is dus 1 - 2sin(x).cos(x) = y2...dus
sin(x).cos(x) = (1 - y2) / 2
De oorspronkelijke vergelijking gaat nu over in:
y = (1 - y2) / 4
y2 + 4y - 1 = 0
y = 0,23606
sin(x) - cos(x) = 0,23606
W(2).sin(x-45) = 0,23606
x - 45 = 9,6 + k360
x = 54,6 + k360 		x - 45 = 180 - 9,6 + k360
x = 215,4 + k360


10.
a.
9sin2(x) + 2cos(3x)(2sin(3x) + cos(3x)) = 2 + 24sin4(x) - 16sin6(x)
Vooraf:
sin(3x) = 3sin(x) - 4sin3(x)............kwadrateren.....
sin2(3x) = 9sin2(x) - 24sin4(x) + 16sin6(x)
de oorspronkelijke vergelijking gaat hiermee over in:
sin(3x).[4cos(3x) - sin(3x)] = 0
sin(3x) = 0.................x = k120....of.....x = 60 + k120
of
4cos(3x) - sin(x) = 0
W(17).sin(3x + 104) = 0
3x + 104 = k360......................x = -35 + k120
of
3x + 104 = 180 + k360..............x = 25,3 + k120
b.
cos x
cos (2 x)
 + 
5 ·  sin x
sin (2 x)
 = 0
cos(x).sin(2x) + 5sin(x).cos(2x) = 0
NB: sin(2x) , cos(2x) ¹ 0
sin(2x), cos(2x0 schrijven als sin(x) , cos(x).............
sin(x).[12sin2(x) - 7] = 0
sin(x) = 0...................x = k180
of
sin(x) = +- 0,76
x = 49,8 + k360........of .....x = -49,8 + k360
of
x = 130 + k360...........of...........x = -130 + k360