floodfill algorithm

a non recursive Floodfill algorithm

21-12-2021:
Version 1.1: Corrected error:
(Drawing blocked in Delphi versions 10,11 caused by not initialized clipping rectangle for XBitmaps)

download tester program

download Delphi project

this project uses some of my own components:

download components

Introduction
This is a new floodfill article, including a much faster exerciser program.
The old article, based on the same algorithm, may be found [here] .

Floodfill is a method to fill a random shape with a pattern.
This floodfill method is implemented in my TXBitmap class.
TXBitmap is a Bitmap with several new features such as

Using drawing levels, a lower level pen cannot overwrite a higher level pixel.
The highest level is 0, the lowest is 3.
Floodfill boundary is formed by pixels having level 0 or 1 (the 2 highest levels).
Pattern drawing is at level 2.
The level of a pixel is stored in blue bits 0,1.

The cliprect is a rectangle on the screen.
Painting outside the cliprect is not possible.

The floodfill algorithm here presented is non recursive.
This is an advantage because, while filling large shapes, stack boundaries cannot be violated.

Below is a reduced picture of the floodfill exerciser at work

Click at the download icon (lightning) icon at the top to load the (Windows) exerciser program.

How to use the floodfill exerciser

Click on a menu button to select an operation:

For lines, ellipses, freehand drawing:
Press left mousebutton, keep pressed and move mousepointer over screen.

To fill, press mousebutton on point to start filling.

Select a pen width, fill color or fill pattern by clicking on the color- ,
pen width- or fill pattern selector.

Tarry's maze algorithm
My floodfill method is based on Tarry's maze algorithm.
In 1895, the mathematician Gaston Tarry published a procedure to escape from a maze.
Mazes were very popular at that time.

Mathematically, a maze may be described by nodes and connections, so by a graph.
A graph is a drawing consisting of points, which may be, or may be not, connected by lines.
The points, or nodes, are road intersections, start- or ending points.
The lines are drawn straight however in reality roads in a maze change direction to confuse the visitor.

Starting at an arbitrary place in the maze, according to Tarry's algorithm,
two distinct signs should be painted along the route

Also, there are two rules that must be obeyed

Figure below shows part of a maze being traversed. The starting node is A.

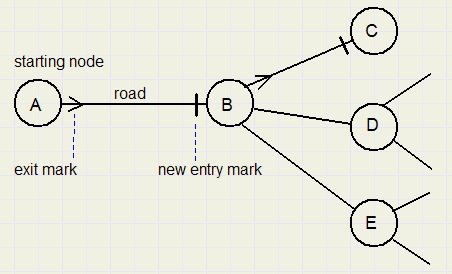
Starting at A, an exit mark is placed. Arriving at new node B, an entry mark is placed.
Choosing the road to C, again an exit mark is placed as well as an entry mark when entering new node C.
If C has no exit roads, the road back to B is taken. At B, a new route, say to D, is choosen, exit mark placed etc.
The road back from B to A may only be taken if all exit routes from B are traversed.
In this way there is certainty that the exit is found.
But if no exit exists, we will eventually return to the starting point.
But in that case, all nodes have been visited.

Algorithm implementation
Pixels on a screen may be considered as a maze, see picture below, where adjacent pixels are connected by roads
in horizontal- and vertical directions.

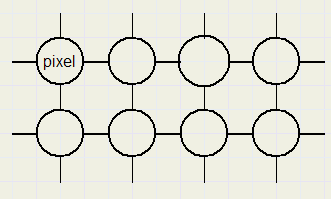
While traversing this maze, for each pixel we need one byte of information
to record the following conditions:

bit	meaning
-01-	direction 0..3 in which pixel was entered
-3-	scan started at this pixel
-4-	pixel scanned
-5-	pixel to be filled

Direction bits:

code	direction	previous pixel
00	right	x := x - 1
01	left	x := x + 1
10	up	y := y + 1
11	down	y := y - 1

Notice that the opposite direction is obtained by 'direction xor 1'

The TXBitmap class uses the pf32bit pixel format.
Here, bits 0..7 hold the blue, bits 8..15 the green and bits 16..23 the red intensity.
Bits 24..31 are unused and here we store the scanning information.

The floodfill procedure is made up of the following parts:

1.Marking of the boundaries

The edges of the cliprect are set to $10, the "scanned" status.

2.Marking level 0,1 pixels

Pixels within the cliprect which have level 0 or 1 are set to the "scanned" condition.

3.Scanning

Mark the starting pixel $38: fill, scanned,start bit.
dir is a byte variable holding the scan direction.
Set dir := 0 and proceed to nextpixel

nextpixel

if pixel[x,y] already scanned: goto previouspixel
not scanned : set scanned, set fill, set entry direction (dir)
if dir = 1: goto nextpixel
if dir <> 1 : dir := 0
(if going left, continue left, else go right)

previouspixel

dir + 1
if dir = entry direction xor 1 : dir + 1
if dir < 4 goto nextpixel
if dir > 3 : dir := entry direction of pixel xor 1, goto previuous pixel
if startpixel: goto fill

fill
The fill pattern is stored before in fillmap : array[0..7] of byte
This is done when selecting the fill pattern.
A pattern is 8 * 8 bits.
A bit set enables the writing of the brush color.
The 8 bits in a byte of the fill pattern correspond with 8 horizontal screen pixels.
If the pattern bit is set, the screen pixel may be written.
The 8 bytes in the pattern correspond to 8 vertical pixels of the screen.
The screen x and y addresses are anded by $7 for comparison with the fill pattern.
See picture below

The screen cliprect area is scanned for pixels having the fill bit set.
If so, the corresponding bit in the pattern is checked.
If set, the brush color is written.
In any case however, the bits 24..31 of the pixel are reset.

the Project

This Floodfill Delpi-7 project has one form and 3 units:

Pixel addressing is by pointers to memory locations.
This bypasses Windows calls and saves considerable time.

For details, please refer to the source code: