numeric solution of a geometry puzzle

The problem

This article describes the numerical solution of a difficult geometric problem.
After completion I managed to find also a geometric solution, see [HERE].

This is the problem:

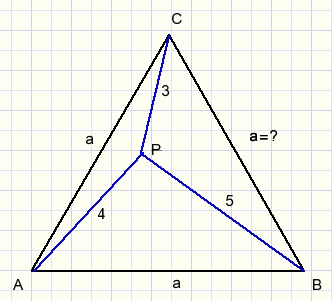
Given is an aquilateral triangle ABC with inside a point P such that:

Asked: length a of the sides.

The solution

We start with a guess for LACP.
With this angle known we may calculate (using the sine rule) LCAP and AC.
Then we know LPAB and in the same manner we may calculte AB.
The guess for LACP was correct if AC = AB.

How to guess LACP in a systematical way?
For this the program uses three variables: angle, amin and amax.
amin is the minimal value of the angle, amax is the maximum value.
angle is the guess for LACP.
angle = (amin + amax)/2.

Now two results are possible:

In case 1. the program sets amax = angle
and is case 2. the program sets amin = angle.
This results in clamping the value of angle between amin and amax, reducing the difference by 50% at each step.
This process repeats until |AC-AB| < 0,000001

Data

const deg2rad = pi/180;
      rad2deg = 180/pi;

type TG3 = record
            a : double;
            b : double;
            c : double;
            alpha : double;
            beta  : double;
            gamma : double;
           end;

procedure triangle(var G3 : TG3);
//given: a,b,alpha
//calculate : c, beta, gamma
begin
 with G3 do
  begin
   beta := arcsin(b*sin(alpha)/a);
   gamma := pi - alpha - beta;
   c := a*sin(gamma)/sin(alpha);
  end; 
end;

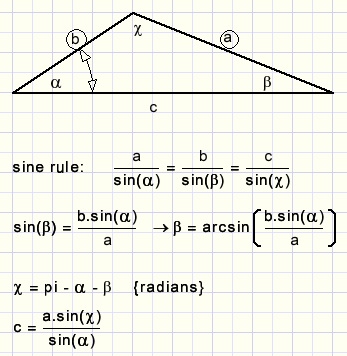
Above procedure is called twice to calculate AC first and then to calculate AB.
This procedure calculates a:

procedure TForm1.Button1Click(Sender: TObject);
var amin,amax,angle,ha : double;
    A1,A2,A3 : TG3;
    x1,y1,x2,y2,x3,y3 : word;
    steps : byte;
begin
 amin := 0; amax := 60; //degrees
 steps := 0;
 with A1 do
  begin
   a := 4; b := 3;
  end;
 with A2 do
  begin
   a := 5; b := 4;
  end;
 with A3 do
  begin
   a := 3; b := 5;
  end;
 repeat
  inc(steps);
  angle := (amin + amax)/2;
  A1.alpha := angle*deg2rad;
  triangle(A1);
  A2.alpha := (60*deg2rad-A1.beta);
  triangle(A2);
  if A1.c < A2.c then amax := angle else amin := angle;
 until abs(A1.c - A2.c) < 1e-6;
 statictext1.Caption := formatfloat('##0.00000',A1.c);
 statictext2.caption := formatfloat('##0.000',angle);
 statictext3.caption := inttostr(steps);
//
 x1 := 300;
 y1 := 150;
 with paintbox1 do with Canvas do
  begin
   brush.Color := $ffffff;
   brush.style := bsSolid;
   fillrect(rect(0,0,width,height));
   pen.Width := 1;
   pen.Color := $000000;
   brush.Style := bsClear;
   ellipse(150,150,450,450);
   ellipse(100,100,500,500);
   ellipse(50,50,550,550);
   pen.Color := $ff0000;
   moveto(300,150);
   x2 := 300-round(50*A1.c*sin(A1.alpha));
   y2 := 150+round(50*A1.c*cos(A1.alpha));
   lineto(x2,y2);
   ha := 0.5*pi - A1.alpha - a1.beta - A2.alpha;
   x3 := x2 + round(50*A1.C*cos(ha));
   y3 := y2 - round(50*A1.C*sin(ha));
   lineto(x3,y3);
   lineto(x1,y1);
   pen.color := $0000ff;
   moveto(300,300);
   lineto(x1,y1);
   moveto(300,300);
   lineto(x2,y2);
   moveto(300,300);
   lineto(x3,y3);
  end;
end;

Below is the result (reduced picture):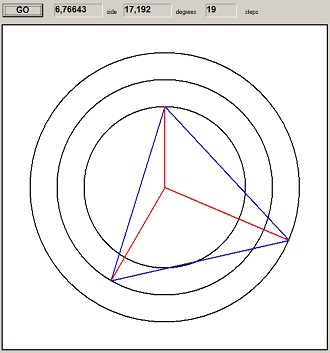

Side a has length 6,766 and the approximation took 19 steps.