geometric puzzles requiring rotation

Geometric problems that require rotation are difficult in general.
This article presents three examples.

Problem 1




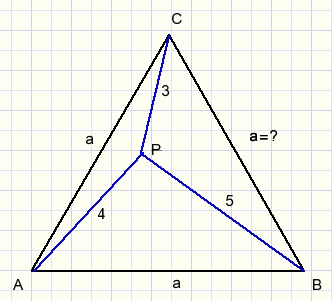
Given is an equilateral triangle ABC with inside a point P such that:
    PC = 3
    PA = 4
    PB = 5
To calculate: the length a of the triangle.

The solution is reached by a 60 degrees counterclockwise rotation of triangle BPC around center B.
After rotation P becomes P', C' = A.
Triangle PP'B is equilateral as well so PP'=5.
Now look at triangle PC'P'.
The sides have lengths 3,4,5 which makes it right-angled (Pythagoras lemma).
After rotation the sides AP and AP' are penpendicular.
So, before rotation their intersection had an angle of 90 + 60 = 150 degrees.(LAPC)



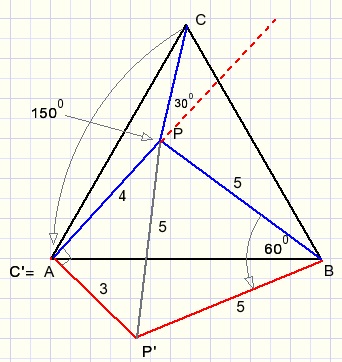
Apply the cosine rule in triangle APC to calculate side AC = a:
    a2 = 32 + 42 - 2.3.4.cos(1500)
    a2 = 25 - 24.(-0,866)
    a = 6,766
See also THIS article where I obtain the same result using
successive approximation, a numerical method.
The program is written in Delphi.

Problem 2




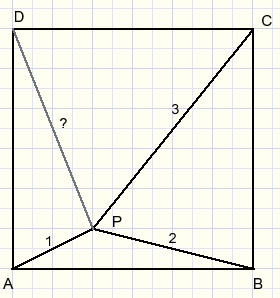
Given is square ABCD with point P inside such that:
    AP = 1
    BP = 2
    CP = 3
Unknown is the side of the square.
Asked: the length of DP.

Two rotations are required:
1.
C is the center. Rotate triangle CPB 90 degrees clockwise.
2.
A is the center. Rotate triangle ABP 90 degrees counterclockwise.



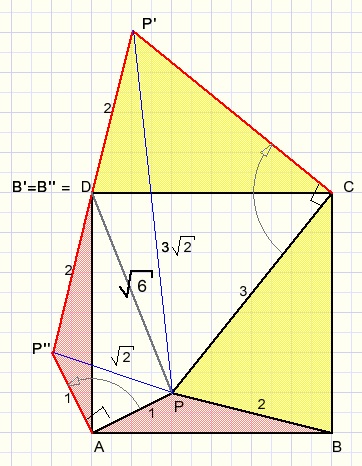
In above figure P'DP'' is a straight line because P'D is a 90 degrees clockwise rotation of BP
and P''D is a 90 degrees counterclockwise rotation of BP.

Triangle PCP' is isosceles and right-angled so calculation of PP' is possible.
The same is true for triangle APP'' and side PP''.
In triangle P''PP' now PD is median and the lengths of the sides are known.
Using the formula for medians (a special case of Stewart's lemma) PD may be calculated.



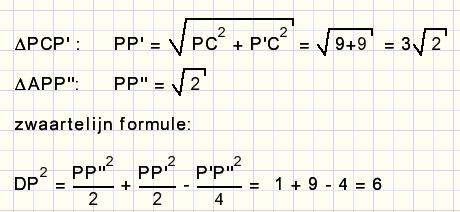
note: "zwaartelijn" is Dutch for median.

Finally:
What length has the side of the square?
Hint:
1. use the cosine rule or
2. realize that pentagon APCP'P'' has the same area as square ABCD

Problem 3




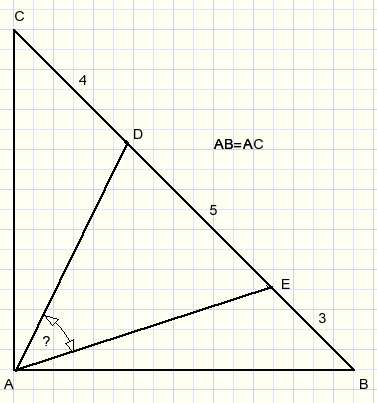
Given is right angled isosceles triangle ABC (AB = AC).
Asked is LDAE.

The 3,4,5 lengths remind of the Pythagoras lemma.
Rotate ABC clockwise 90 degrees using A as the center of rotation.
So:
    C becomes C'= B
    D --> D'
    E --> E'
see picture below:



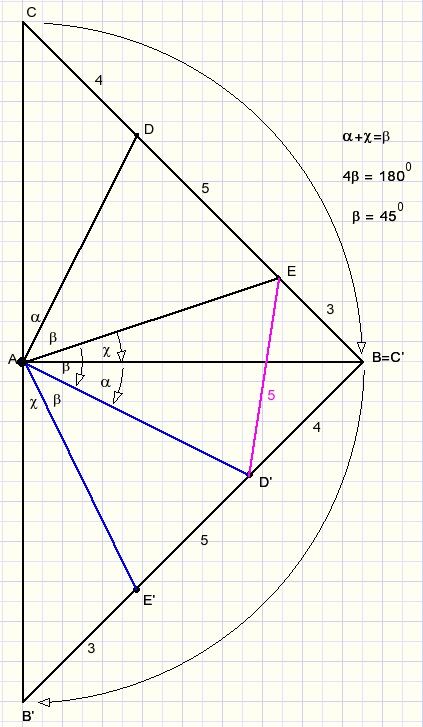
Because AD'= AD and D'E = 5, triangles ADE and AD'E are congruent.
Also notice that:
    LCAD = LC'AD'
    LEAB = LE'AB'