

| Programming a 3D Tic Tac Toe game |
 return to TicTacToe page.
return to TicTacToe page. see Delphi unit1
see Delphi unit1 see Delphi unit2
see Delphi unit2 download complete Delphi project
download complete Delphi projectIntroduction
This article describes a Delphi programming project of a 3 dimensional tic-tac-toe game.It is a two player version, however, for a single player it may be interesting to find a winning strategy.
A game state may be analysed: per field a calculation is made that predicts
the result of a move in that field (e.g. winning in 5 moves, losing in 7 moves).
This game is simple, as is the program. However, in the case of more complex games having
menus to choose from, single and dual player options or several game levels, the same structure may be used.
Also the analyses procedure is applicable to a wide variety of games.
Therefore this project is a general blueprint for board games.
The Delphi(7) project has one form and two units.
Form1 holds the game and three images used as buttons.
Unit1 handles events, paints the game and contains the procedures to control the game.
Unit2 has the data for the game, moves and the procedures for game analysis.
The game
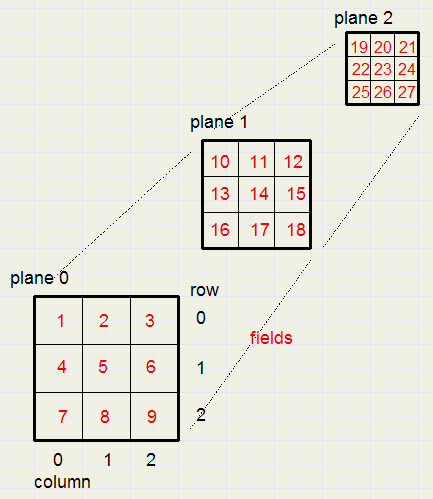
The breakdown into plane, row and column are only for the purpose of drawing and
the conversion of mouse-coordinates to field number.
The game is drawn in paintbox1 and the next data supplies all information
type TPlane = record
left : word;
top : word;
square : word;
end;
const planes : array[0..2] of TPlane =
((left : 20; top : 450; square : 80),
(left : 280; top : 220; square : 70),
(left : 510; top : 20; square : 60));
fw = 9; //frame width
gameBGcolor = $feffff;
markcolor = $00b0ff;
chdef : array[1..2] of char = ('O','X');
playercolors : array[1..2] of dword = ($0000ff,$ff0000);
left, top are relative to the paintbox.square is the length in pixels of a field.
The boardstate is recorded in array game
const maxmove = 27; ..... var game : array[0..maxmove] of byte; //1=O 2=Xnote: game[0] is not used.
The moves should be recorded in a list for the case of backward moving and also for analyses.
type TNode = record
pos : byte;
rating : byte;
treshold : byte;
end;
......
var node : array[1..maxmove] of TNode;
moveNr : byte;
pos is the move position (field).rating and treshold are for analyses and will be explained later.
Conversions
Field numbers have to be converted to plane,row and column and vice versa.
type TPosTriple = record
column : byte;
row : byte;
plane : byte;
end;
........
function pos2triple(p : byte) : TPosTriple;
//convert position p to column,row,plane
begin
with result do
begin
dec(p);
column := p mod 3;
p := p div 3;
row := p mod 3;
plane := p div 3;
end;
end;
......
function triple2Pos(tr : TPosTriple) : byte;
//convert column,row,plane to position
begin
with tr do result := column + 3*row + 9*plane + 1;
end;
The position must also be converted to the field rectangle
function pos2Rect(p : byte) : Trect; //calculate rectangle of a field [1..27] var tr : Tpostriple; begin tr := pos2triple(p); with tr do with planes[tr.plane] do begin result.left := left + square*column; result.top := top + square*row; result.Right := result.Left + square; result.Bottom := result.Top + square; inc(result.Left,fw); dec(result.Bottom,fw); end; end;note: fw is the width of the game edges. Purpse is to have a 3 dimension look.
The rectangle is limited to the area excluding the edges.
When moving the mouse pointer over the paintbox, the (x,y) mouse coordinates must be converted
to a field number. A field of 0 is supplied if no field or an allready occupied field is covered.
function xy2field(x,y : word) : byte;
//convert mousex,y to field
//no field = 0
var hit : boolean;
r : Trect;
i : byte;
begin
hit := false;
i := 0;
while (hit = false) and (i < maxmove) do
begin
inc(i);
r := pos2rect(i);
hit := (x > r.Left) and (x < r.Right) and
(y > r.top ) and (y < r.Bottom);
end;//while
if hit then result := i else result := 0;
end;
Painting the game
Painting includes the painting of the frame, of the player moves and marking/unmarking winning triples.The frame is painted fw (framewidth) pixels wide to obtain a 3D effect.
Procedure multiline paints 3D lines.
procedure multiline(x1,y1,x2,y2: word; w : byte; colr : dword);
//paint w fold line (x1,y1) --> (x2,y2) in paintbox1
var i : byte;
begin
with form1.PaintBox1.Canvas do
begin
pen.Width := 1;
pen.Color := colr;
for i := 0 to w-1 do
begin
moveto(x1+i,y1-i);
lineto(x2+i,y2-i);
end;
end;
end;
procedure paintframe;// paints the edges of the game procedure paintfield(..) paints a field with "O" or "X" procedure paintgame;// paints all fields procedure markwinner;// paints background color of winning fields procedure unmarkwinner;// paints original background color of winning fields
Winning
type TWintriple = record
p1,p2,p3 : byte;
end;
A wintriple are three adjacent "O" or "X" marks.p1, p2, p3 are the game fields.
A list winlist holds all triples that make a winning board state.
var winlist : array[1..50] of TWinTriple;
wincount : byte;
wincount holds the number of entries in winlist[ ]The winlist is generated at creation time.
Originally I designed a quite complicated procedure to generate the winlist, but later a more simple one
struck my mind.
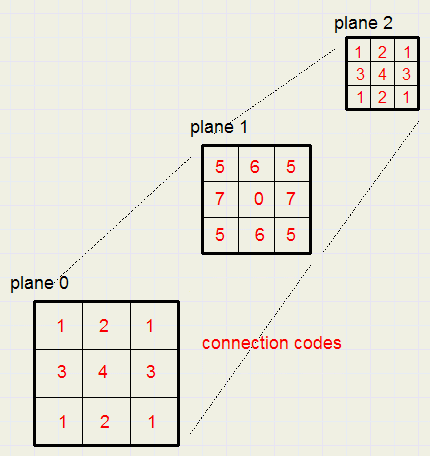
The middle field simply is the average value of both.
By marking each field by a number, which is the same when they form a starting and ending field,
generation is simple.
procedure makewinlist;
const concode : array[1..maxmove] of byte =
(1,2,1,3,4,3,1,2,1,5,6,5,7,0,7,5,6,5,1,2,1,3,4,3,1,2,1);
var i,j : byte; //start..end field
begin
wincount := 0;
for i:= 1 to 25 do
for j := i+2 to 27 do
if concode[i] = concode[j] then
begin
inc(wincount);
with winlist[wincount] do
begin
p1 := i;
p2 := (i + j) shr 1;
p3 := j;
end;
end;
end;
The concode (connection code) number allows for the triples.By having index j starting from i+2, double generation is avoided.
The procedure below returns true if the game holds a winning triple.
function checkwin(var tr : TwinTriple; player : byte) : boolean;
//check for win somewhere, return wintriple# tr
var i : byte;
begin
i := 0;
result := false;
repeat
inc(i);
with winlist[i] do
result := (game[p1] = player) and
(game[p2] = player) and
(game[p3] = player);
until result or (i = wincount);
if result then tr := winlist[i];
end;
Game control
A game has certain states or situations.Responses to user input (keyboard,mouse) are situation dependent.
type TGameStatus = (gsInitializing,gsAnalysing,gsMoving,gsEnd);
TGameUpdate = (guMove,guWin,guAnalyseBtn,guNewBtn,guBackBtn);
.....
var gamestatus : TGamestatus;
Only in the state gsMoving, mouse and keyboard events are honoured.guMove is the result of a mouseclick in an empty field.
Button clicks result in a gameUpdateMessage to Game Control. (guAnalyseBtn,guNewBtn,guBackBtn).
So, a model to handle these things is a table-like structure where the events are the columns
and the game states are the rows.
At the intersection of columns and rows are handling code or procedure calls to accomplish a task.
This translates to nested case statements.
Similar structures arise in many other cases and this approach generates comprehensible code.
Note, that this game is very simple, but others may be not.
procedure GameControl(gum : TGameUpdate);
begin
case gamestatus of
gsMoving : case gum of
guMove : moveproc;
guBackBtn : backproc;
guAnalyseBtn : analyseproc;
guNewBtn : newproc;
end;//case
gsEnd : case gum of
guNewBtn : newproc;
guBackBtn : backproc;
end;//case
end;//case
end;
Nice is, that the origin of a guXXX message may be keyboard as well as mouse.The GameControl procedure has several helpers, that take care of the necessary actions.
(moveproc, backproc, analyseproc).
Please refer to the source code of unit1 for the details.
Game analyses
Pressing the analyses button in the game, supplies the prediction per field for that move.Typical is W3 for winning in three or L6 for losing in six moves.
During the game, moves are stored in the .pos field of the node (type TNode)
TNode = record
pos : byte;
rating : byte;
treshold : byte;
end;
.....
var node : array[1..maxNode] of TNode;
moveNr : byte;
moveNr is the last move done by a player.pos is the field of the move (1..27)
The player number (1 for "O" , 2 for "X") is obtained from moveNr
player := 2 - (moveNr and 1);Analyses involves a large number of trial moves and registration of the results (wins).
These trial moves (not displayed) are also registered in array node[ ].
Two more variables are added to control this process
var baseNode : byte;
testnode : byte;
baseNode := moveNr + 1, so, the next free node, which holds the first trial move.(btw : node is a math phrase from graph theory.
A node is typically a place where many roads originate or come together.
For "road", read "move".)
TestNode is the number of a trial move.
So, testNode runs from baseNode to 27 (maxmove).
Basically, the analyses procedure is of the so called "brute force" type.
This means, that all possible combinations of moves are generated.
However, without some tricks, analyses would require unacceptable long times.
Trial move counting
To test all possible sequences of moves, the analyser uses the following scheme:(suppose an empty game, baseNode = 1)
move node 1 2 3 4 5 6 7 8 9 1 1 2 1 2 3 1 2 3 4 1 2 3 4 5 1 2 3 4 5 6 1 2 3 4 5 6 7 1 2 3 4 5 6 7 ........and "O" winsNotes:
1. Remember, that nodes 1,3,5,7,.. are "O" and nodes 2,4 6,8,.... are "X"
2. If fields were occupied by former moves, they would be skipped.
For each new trial move the first empty field is selected.
Say that we start analyses at node 25 and no winning takes place.
Free fields are 2, 14 and 25.
After 3 trial moves:
node 25 26 27 pos 2 14 25No more moves are possible. Field 25 removed, node 26 updates the move to 25, the next free field.
Then node 27 selects the only empty field 14
node 25 26 27 pos 2 25 14Then field 14 is removed, node 26 cannot find a next empty field and therefore removes field 25.
Then node 25 selects the next free field 14, node 26 selects field 2, node 27 selects field 25
node 25 26 27 pos 14 2 25The fields (stored in node[....].pos) form a counter.
The last "number" being
node 25 26 27 pos 25 14 2When node 25 (baseNode) is unable to update it's move ( all moves done), the analyses procedure exits.
Rating
Somehow, we have to remember the "success" of a particular move.The best, of course, is winning.
But also good is winning in 4 or 6 moves.
Losing in 7 moves is less worse then losing in 3 moves.
Nodes have a field called rating which is a number 1..100.
The meaning is
rating meaning 1 losing in 1 move 3 losing in 3 moves 5 losing in 5 moves ....... 50 neutral, no winning or losing ....... 96 winning in 4 moves 98 winning in 2 moves 100 winning moveA higher rating is always better.
If node 15 wins, it's rating is set to 100 and control is transferred to the previous node 14.
x := 100 - node[testNode].rating; if x > 50 then dec(x); if x < 50 then inc(x); dec(testNode); if x > node[testnode].rating then node[testNode].rating := x;So, if the rating of node 14 was 0, it now becomes 1 (losing in 1 move).
The rating of a node may only increase.
Each node tries to obtain the highest possible rating.
So, node 14 selects the next move and opens node 15.....and so on.
If no move is possible at the highest node, the rating is set to 50.
if a node is out of moves, it transfers control to the previous node.
This scheme works allready, move results can be predicted, but the process is extremely slow.
Time for some tricks for a dramatic speedup.
Speeding up analyses
1.Say node n has rating 94 (win in 6 moves) and then node n+1 updates it's rating from 0 to 5.
This 5 would generate rating 94 for node n when node n+1 closes.
However, node n allready has this rating.
For node n+1 it is meaningless to search for any higher rating, say 90, which would present a rating
of 11 to node n: the rating 94 would not change.
Therefore, there are cases where the combination of ratings of two successive nodes results in closing of
a node and transferring control to the previous node.
This is called a shortcut.
2.
Instead of comparing ratings of two successive nodes, it is convenient to transfer the rating of node n to node n+1.
This new value is called the treshold
So from now, a node may compare it's rating to it's treshold.
If the rating is equal or exceeds the treshold, control is transferred to the previous node.
3.
Say, node 10 has rating 96 (winning in 4 moves = winning at node 14).
A better rating implies winning in a lower node. So, it is useless to search for any further moves beyond node 12.
As will be explained, the treshold takes care of that.
4.
The nodes form a tree, which is a graph without loops.
Note: in math, a graph is a figure with dots, which may be (or not be) connected by lines.
A graph is an abstract image.
Graphs are widely used in industrial planning, roadmaps, file systems, chemistry and computer games.
Actually in all circumstances where dependencies exist or changing states..
The number of combinations (moves, routes) is very high.
The more nodes are involved, the longer the analyses will take.
A good way to limit the depth is to search for any win just after opening a new node, so
first try every move for a win after actually doing the first trial move.
At a win, control is returned to the previous node, so the search depth is limited.
Analyses: Putting things together
moveNr is the last player move.Pressing the analyse button wil
-
- set baseNode to moveNr + 1
- set testNode to moveNr
-
- nextNode
- test for win
- firstmove
- previousnode
- nextmove
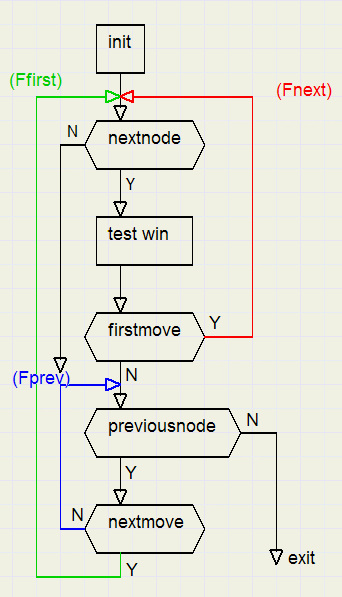
There are three loops, implemented by while statements
-
- nextnode --> testwin --> firstmove --> nextnode ...controlled by boolean variable Fnext
- previous node --> no next move --> previous node...controlled by Fprev
- nextmove --> nextnode .....controlled by Ffirst
procedure analyse;
//analyse game
var Ffirst,Fnext,Fprev : boolean;
begin
if movenr = 27 then exit;
testNode := moveNr;
baseNode := moveNr + 1;
Ffirst := true;
while Ffirst do
begin
Fnext := true;
while Fnext do
begin
Fnext := false;
if nextNode then
begin
testwin;
Fnext := firstMove;
end;
end;
Fprev := true;
while Fprev do
if previousNode then
begin
if nextmove then Fprev := false;
end
else begin
Ffirst := false;
Fprev := false;
end;
end;//Ffirst
end;
NextNode
If there is no next node (in case of node 27) then exit false.Else, increase testNode and initialize rating and treshold of the new node:
exit false if testnode = 27
testnode + 1
pos := 0 {no move yet}
baseNode --> treshold := 100; rating := 1
not basenode -->
x := 100 - rating previous node
x > 50 --> x + 1
x < 50 --> x - 1
testnode >= 26 --> treshold = 50
testnode <> 25 --> treshold := x
x := 100 - treshold previous node
x > 50 --> x + 1
x < 50 --> x - 1
rating := x
exit true
The treshold := 50 trick at node 26 will be explained later.Test win
There is a difference of checking for the basenode and the higher nodes.Searching and comparing the winlist[ ] with the game[ ] will stop for the higher nodes if a win is found.
For the basenode however, all fields on the board are checked,
winning triple numbers are displayed in array[1..27] scores.
This is because we want to know every field where to win.
Testwin sets the rating of node[testnode] to 100 in case of a win.
FirstMove
if treshold = 100 --> treshold := 98 {no win found}
result := rating < treshold;
if result
find free field
set game[field]
set pos to player ( 1 for "O", 2 for "X"}
Previous node
This is the most complicated partVariable prf (boolean) is true as long as the previous node is taken
which is the case when the updated rating equals or exceeds the treshold
result := false
prf := true
while prf
prf := false
delete move
testNode > basenode -->
result := true {else result := false}
x := 100 - rating
testnode - 1
x > 50 --> x - 1
x < 50 --> x + 1
testNode = baseNode --> report rating
testNode > baseNode -->
x > rating --> rating := x
prf := rating >= treshold
end//while
Next move
After selecting the previous node, this function tries to do the next move of this node
result := false
delete move
find next free field --> result := true
set game[free field]
please refer to the source code for details.Each node tries to obtain the highest possible rating.
The previous node is selected if a higher rating does not change the rating of the previous node.
This avoids examination of millions of moves and is therefore the biggest time saving trick.
An exception is the baseNode: the rating is kept down to 1 so all moves are examined.
Picture below shows the algorithm for successive moves without wins.
Initially the treshold of a new node is set to 100, no win sets the treshold to 98
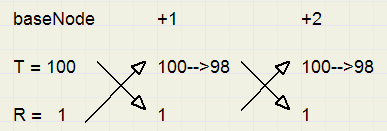
The nodes 26,27 treshold trick
In node 26,27 the treshold is standard set to 50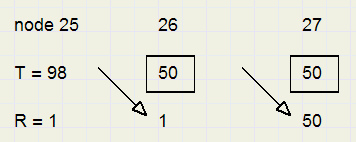
Below is pictured a winning situation at baseNode + 3, node +2 has done all it's moves without
improving it's rating, node +1 rating equals it's treshold so returns to the baseNode.
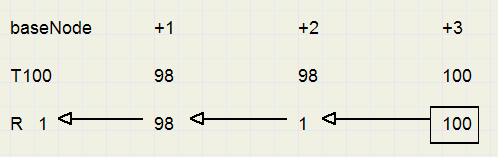
Search depth reduction
The algorithm automatically takes care of unnessary search depths.Assume node 15 has found a rating of 94 (winning in 6 moves) long ago and now tries to improve this
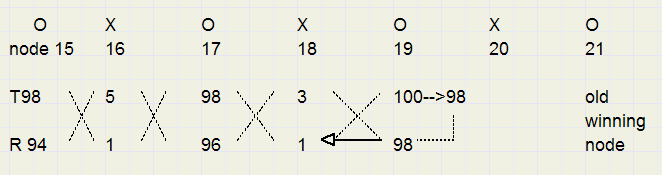
The rating now equals the treshold so the previous node is selected.
Of course it makes no sense to search any further, as before a winning situation was found at node 21.
This concludes the description of 3D tic-tac-toe.
The analyses algorithm is applicable to all board games, only the testwin procedure will be different.
In single player games, the algorithm may search for the best computer move.
Donations
In case you make commercial use of the analyses algorithm, do not forget a donation for my website.Please contact me for details.

