

| Sudoku Oplosser |  |
Dit is versie 2.0 van mijn Sudoku oplosser.
De knopjes zijn wat handiger geplaatst.
 |
| verkleinde weergave van de Sudoku oplosser |
Inhoud
Sudoku-Kraker Hulp
-
Programma mogelijkheden
Bediening
Een nieuw spel invoeren
Zelf oplossingen zoeken
Een spel laten oplossen
Een spel opslaan
Een spel openen
Mogelijkheden met de Sudoku-Kraker
De Sudoku-Kraker is een (Windows) programma dat voorziet in-
- assistentie bij het zoeken door opties te tonen
- spel analyse met 3 verschillende strategieën
- oplossen van zelfs de moeilijkste puzzels
- onderzoeken of er meer oplossingen bestaan
- handmatig een nieuw spel invoeren
- zelf oplossingen zoeken
- handmatig opties verwijderen
- openen en opslaan van Sudoku puzzels
De knoppen
Deze menu knoppen staan boven in het scherm:| - openen | : klik om een eerder opgeslagen spel te openen |
| - opslaan | : klik om een spel te bewaren |
| - help | : klik om deze pagine te openen |
| - nieuw spel | : klik om een handmatig een nieuw spel in te voeren |
| - play | : klik om zelf oplossingen te zoeken |
| - analyse | : klik om hints te ontvangen |
Een nieuw spel invoeren
Klik op de nieuw spel tekst.De oranje cursor wijst naar het veld dat ingetikte cijfers plaatst.
De kleur van de cijfers is bruin, een origineel cijfer dat later niet gewijzigd kan worden.
Verwijder een cijfer door de cursor op het veld te plaatsen en de delete toets in te drukken.
De cursor is te verplaatsen met de cursor toetsen, spatiebalk en de backspace toets.
Als de opties (checkbox midden rechts) aan staan dan kan ook met de muis op een optie geklikt
worden om het cijfer in te voeren.
Klik op de clear knop rechts onder om alle cijfers te wissen.
Zelf oplossingen zoeken
Klik hiervoor op de play tekst rechtboven.De ingetikte cijfers hebben de kleur zwart: cijfers van de speler.
De cursor bepaalt waar het cijfer komt te staan.
Wis een cijfer door de cursor op het veld te plaatsen en de delete toets in te drukken.
Klik op de original knop rechtsonder om alle zwarte cijfers te wissen.
Als de opties aan staan dat kan nog het volgende:
-
- een linker muisklik op de optie plaatst dat cijfer
- een rechter muisklik op een optie verwijdert die optie
- een cijfer intikken in een veld zonder die optie herstelt die optie
Hulp bij het oplossen
1. Brute kracht oplossingenKlik op de play tekst rechts boven.
Klik op oplossen knop er onder.
Dit lost alle Sudoku puzzles op, hoe moeilijk ook.
De nieuwe cijfers hebben de kleur oranje.
Klik opnieuw op oplossen om nog meer oplossingen te zoeken.
(Een goede puzzel heeft 1 unieke oplossing).
Als meer oplossingen worden gevonden dat is de puzzel fout.
Klik op de org.speler knop rechtsonder om de oranje cijfers te verwijderen.
Dit herstelt het spel op het punt van de laatste zet van de speler.
2. Assistentie bij het oplossen.
Klik op de analyse tekst om een hint te ontvangen.
Alle analyse methoden proberen overbodige opties in de velden te vinden
om die te verwijderen.
Na de hint staat de tekst "doorgaan:
Met herhaaldelijk drukken op de spatiebalk (en analyse geselecteerd,
wordt de ene na de andere hint uitgevoerd totdat het spel is opgelost.
Steeds wordt duidelijk aangegeven waarom een conclusie wordt getrokken.
Er zijn 3 soorten van aanpak:
A.
Optie reductie binnen een rij, kolom of groep, zie het volgende plaatje:
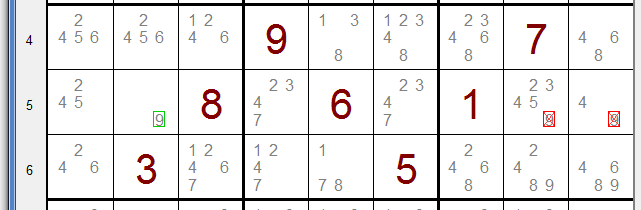
Rij 5, kolom 2 heeft alleen de optie "9".
Hier moet dus de "9" van rij 5 staan en in de andere velden kan die optie worden verwijderd.
De te verwijderen opties zijn rood omrand met een rood kruis.
Zie ook het volgende voorbeeld:
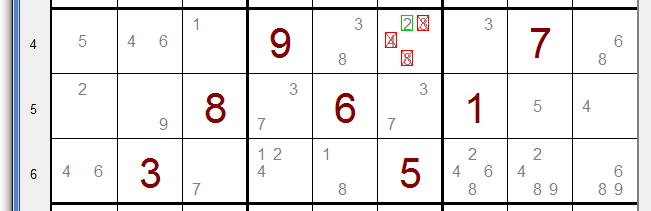
Rij 4, kolom 6 is het enige veld van rij 4 dat een "2" optie heeft.
De andere opties van dat veld kunnen dus worden verwijderd omdat de "2" er moet staan.
Uiteraard zijn soortgelijke situaties mogelijk voor de kolommen en groepen.
Dit zijn trouwens simpele voorbeelden van een algemene regel.
Zie strategie voor een uitgebreide uitleg.
Bovenstaande regels zijn i.h.a. voldoende om 2 (**) tot 4 (****) sterren sudoku's op te lossen.
B.
Optie reductie door interactie tussen groepen en rijen/kolommen.
Kijk eens naar het volgende plaatje:
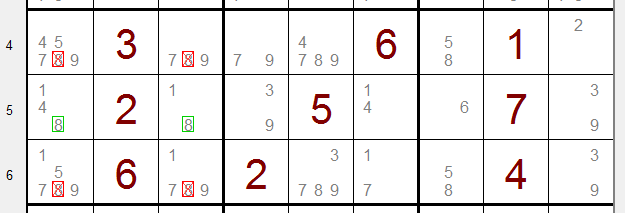
We zien 3 groepen van elk 3*3 velden.
Een groep bestaat uit 3 horizontale drietallen (opvolgende velden in de rij)
Kijk naar rij 5:
De optie "8" staat alleen in kolommen 1 en 3.
Een veld van drietal 2 van deze groep krijgt dus het cijfer "8".
Daarom kan de optie "8" niet voorkomen in drietallen 1 en 3.
Ook hier zijn weer vele variaties mogelijk zoals vertikale drietallen.
Bij strategie staat een uitgebreide uitleg.
Bovenstaand voorbeeld is afkomstig uit een 9 sterren sudoku.
Tot 5 sterren sudoku's komt deze situatie weinig voor.
C.
Als methoden A. en B. geen reductie opleveren dan wordt in elk veld elke optie uitgeprobeerd.
Het tijdelijk ingevoerde cijfer veroorzaakt reducties als methode A. wordt toegepast.
Is het cijfer fout dan ontstaat daardoor ergens een veld zonder opties.
Zie dit voorbeeld:
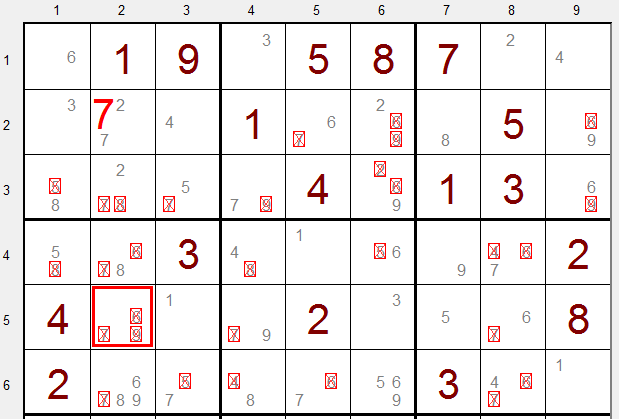
De "7" is tijdelijk ingevoerd bij rij 2, kolom 2.
Na reductie verloor het veld op rij 5 kolom 2 alle opties.
De "7" optie kan dus nooit een oplossing zijn en moet worden verwijderd.
Met deze methode kunnen zelfs 12 sterren Sudoku's moeiteloos worden opgelost,
waarbij elke logische stap wordt getoond.
Klik op de stop knop om op elk moment de assistentie te stoppen.
Een spel opslaan
Klik op de save menu knop en volg de aanwijzingen in het dialoog venster.Bestanden krijgen de extensie .sdk.
Een spel openen
Klik op de open menu knop en volg de aanwijzingen in het dialoog venster.Ook kan een *.sdk bestand dubbel worden aangeklikt.
De eerste keer zal Windows om een applicatie vragen.
Verwijs dan naar het bestand sudoku-kraker.exe.
Daarna worden de *.sdk bestanden met het sudoku-kraker icoon getoond.
Beschrijving van Suduko
Sudoku is een cijfer puzzel.Er zijn 9*9 velden, georganiseerd als 9 rijen, 9 kolommen en 9 groepen (van 3*3 velden).
In een opgeloste puzzel staat in elk veld een cijfer 1 tot 9 zodanig dat in elke rij, kolom of groep
een cijfer één maal voor komt.
Een spel heeft bij aanvang minimaal 17 en maximaal tot zo'n 30 reeds ingevulde cijfers.
De speler moet de lege velden invullen door zoeken en logisch redeneren.
Sudoku puzzels zijn er in sterk uiteenlopende graden van moeilijkheid.
In de krant aangetroffen exemplaren zijn meestal 2 (**) of 4 (****) sterren.
De beschreven A. methode van optie reductie volstaat meestal voor de oplossing.
Bij de 4 sterren puzzels is het alleen wat moeilijker zoeken omdat er minder reductie mogelijkheden zijn.
Door de weergave van opties in lege velden wordt het oplossen een stuk eenvoudiger.
Strategie
Hier volgt de uitleg bij de eerder genoemde A. en B. reductie methoden.A.
De eenvoudigste manier om een sudoku puzzel op te lossen is te beginnen bij een leeg veld
om te proberen welke cijfers daarin passen.
Als er maar één cijfer past (niet conflicteert met ander kolommen, rijen of groepen)
dan kan het cijfer worden geplaatst en dezelfde opties in de rij, kolom of groep worden verwijderd.
Een andere manier is om met een cijfer te beginnen en te proberen waar in een rij (kolom, groep) het past.
Als het cijfer maar in één veld past dan kan daar het cijfer worden geschreven,
wat automatisch andere opties in dat veld elimineert.
Bovenstaande methodes zijn simpele voorbeelden van één algemene regel.
Kijk eens naar het volgende plaatje:

Opties 7,9 komen alleen voor in kolommen 3,4.
Daar moeten dus ook de cijfers 7,9 komen, dwz in andere velden van de rij kunnen die opties worden verwijderd.
Dit is de algemene regel:
Als we K velden selecteren en die velden hebben samen K opties,
dan kunnen die opties niet in andere velden (dan K) optreden.
Alle K opties bij andere velden kunnen worden geschrapt.
Voor K = 1: één optie per veld dropt die optie in de 8 andere velden (van die rij, kolom of groep).
Voor K = 8: 8 velden met 8 opties. De negende optie (cijfer) komt dus alleen in het ene veld buiten K voor.
Dit is het voorbeeld van "cijfer past maar op één plek".
In makkelijke (**) puzzels komt het geval K=1 het meest voor en minder k=8.
De moeilijker (****) puzzels hebben meer K=8 gevallen.
K=2 komt bij weer moeilijker puzzels voor, vanaf 4 sterren.
K=3 zien we sporadisch bij puzzels vanaf 6 sterren.
B.
Dit is de interactie tussen groepen en rijen/kolommen.
We beschouwen nu een spel als groepjes van 3. Dat kan zijn horizontaal of vertikaal.
Een groep bestaat uit 3 horizontale of 3 vertikale drietallen, hoe je het maar bekijkt.
Een rij heeft 3 horizontale drietallen, een kolom heeft 3 vertikale drietallen.
Bekijk nu het volgende plaatje:
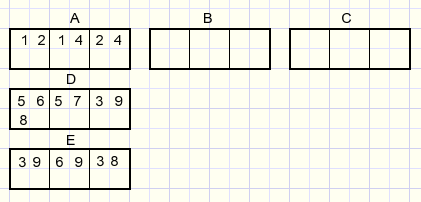
Drietallen ADE vormen een groep. Drietallen ABC vormen een rij.
Opties 1,2,4 komen voor in drietal A en niet in drietallen D of E.
Daarom kunnen deze cijfers nooit voorkomen in drietallen B,C van de rij.
Laten we drietallen B,C en D,E complementair noemen (ze delen drietal A om een rij of groep te maken).
Dit is de algemene regel:
Complementaire drietallen hebben dezelfde opties.
Gevolg: opties die in de een voorkomen maar niet in de ander kunnen verwijderd worden.
In het voorbeeld: opties die niet in drietallen DE staan kunnen niet voorkomen in BC.
Afwezige opties in BC kunnen niet in DE staan.
Installatie
Sudoku-Kraker is freeware en werkt onder alle Windows versies.Er is geen installatie procedure.
Download het Suduku-Kraker.exe bestand en plaats het in een map naar keuze.
De programmeertaal is Delphi (7).
Source Code
Geïnteresseerd in de source code?Kijk [ HIER ].
Er zijn bovendien een aantal sudoku puzzels bijgevoegd, waaronder de moeilijkste ter wereld.
Een sleutelrol in de Sudoku oplosser vervult de combinatie teller, een routine die
systematisch 1..4 velden van de 9 kiest voor analyse.
Kijk [ HIER ] voor een beschrijving.
Veel plezier gewenst!

