

 |
how to paint circles and ellipses (part 4) |  |
 |
contents
| part1 | modifying pixels in a bitmap |
| part2 | drawing dots and lines: the XBitmap class |
| part3 | flicker free painting |
| part4 | drawing circles and ellipses |
Introduction
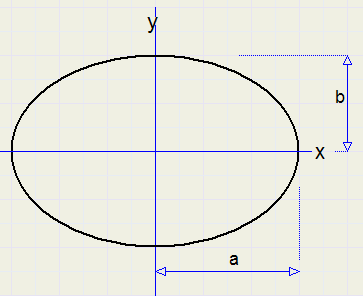
This article describes a way to paint circles and ellipses in the Delphi programming language.Please look at the picture below:
| 2 | |||||||||
| |||||||||
| 2 | |||||||||
| |||||||||
In case of a circle, where a = b = r (radius), the equation becomes x2 + y2 = r2
For the convienience of calculations we assume the center of the ellipse at (0,0).
The ellipse is painted point by point.
To avoid unpainted "holes" between pixels, the slope of the tangent must be observed.
If the tangent is < 1 (and > -1) , a horizontal oriented line , the x coordinate steps by 1
and the corresponding y is calculated.
However, if the tangent is > 1 (or < -1) , a vertical oriented line, then y must be stepped by 1 and x is calculated.
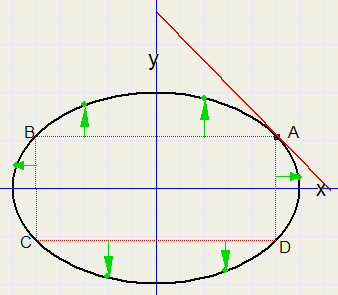
So we first calculate the point on the ellipse where the tangent = 1 (or -1):
| 2 x |
| a 2 |
| 2 y y' |
| b 2 |
If y' = -1 we get......
| x |
| a 2 |
| y |
| b 2 |
| b 2 x |
| a 2 |
Substitution of y in the original equation of the ellipse:..............
| x 2 |
| a 2 |
| b 2 x 2 |
| a 4 |
a 2 x 2 + b 2 x 2 = a 4
| x | = |
|
| y | = |
|
So these are the coordinates of point A.
In case of a = 3, b = 2...........x = 2.496..........y = 1.109
Because of the symmetry we also know points B,C,D.
The ellipse is painted while walking (stepping pixel by pixel) road AB, BC,CD,DA while calculating
and painting the corresponding point of the ellipse.
On AB or CD, x is stepped by 1 and Y is calculated.
On BC or DA, y is stepped and x is calculated.
The program
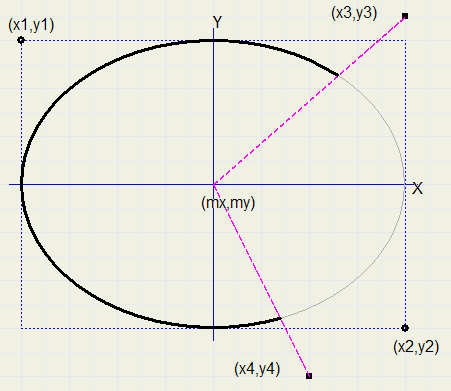
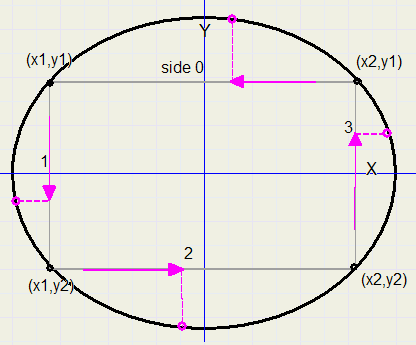
The procedure presented below is part of the XBitmap class and it allows for painting an ellipse arc.The ellipse is defined by it's fitting rectangle with left top (x1,y1) and right bottom (x2,y2).
Calculated center point is M.
Starting point of the arc is the intersection of the line through M and (x3,y3) with the ellipse.
Ending point is the intersection of the line through M and (x4,y4) with the ellipse.
Acode is the arrowcode. If zero, no arrows are painted.
I have removed the code for the arrows.
Also removed is the code to paint dash-dot patterns.
Initially, (x1,y1) and (x2,y2) are the coordinates of the fitting rectangle, but later in the program
(x1,y1) ....(x2,y2) become coordinates of points B and D.
Rectangle ABCD is called the "inner rectangle" in the program comments.
Line AB is coded as side 0, BC is side 1, CD is side 2 and DA is side 3
The Xarc procedure has some local functions and procedures:
procedure nextpoint(var p : integer; var side : byte);
Variable side has a value of 0..3 for AB ..DA.
p is the x or y position on the side.
To know the next point, p is decremented on sides 0 and 3 and incremented on sides 1 and 2.
nextpoint calls procedure nextside.
procedure nextside(var p : integer; var side : byte);//p : point, s : side
If the position p on a side exceeds the length of the side, the side and position must be updated.
Then nextpoint calls itself, because a side may be crossed again in case of a very flat ellipse.
function WtoP(p : integer; side : byte) : TPoint;
This procedure calculates the point on the ellipse to be painted from the side and
position p on the side.
Painting starts at beginside at point sp.
Painting ends at endside at point ep.
XBitmap procedure Dot(.. ,..) paints the point of the ellipse.
Refer to the XBitmap source code for the Dot( ) procedure.
Here also mx and my are added to the point. (pt.x + mx, pt.y + my).
Source code listing
procedure TXBitmap.Arc1(x1,y1,x2,y2,x3,y3,x4,y4 : integer; acode : byte);
//common code for Xellipse,Xarc
//acode = 0 for ellipse, = FXArrowcode for Arcs
//draw arc inside rect(x1,y1)..(x2,y2)
//from intersection with line M..(x3,y3)
//to intersection with line M..(x4,y4) ...counterclockwise
//use penwidth, pencolor, penlevel
var a,b,a2,b2,mx,my,x,y,pa : integer;
beginside, endside : byte;
ab2,s,v1,v2,dab,dba : single;
sp,ep : integer; //start-,endpoint
pt : TPoint;
procedure nextside(var p : integer; var side : byte);//p : point, s : side
//use points x1,x2,y1,y2 as reference ,
//walk (x2,y1)..(x1,y1)..(x1,y2)..(x2,y2)..(x2,y1) side 0..3
begin
case side of
0 : if p = x1 then begin
p := y1; side := 1; nextside(p,side);
end;
1 : if p = y2 then begin
p := x1; side := 2; nextside(p,side);
end;
2 : if p = x2 then begin
p := y2; side := 3; nextside(p,side);
end;
3 : if p = y1 then begin
p := x2; side := 0; nextside(p,side);
end;
end;//case
end;
procedure nextpoint(var p : integer; var side : byte);
//calculate next point and side
begin
if (side = 0) or (side = 3) then dec(p) else inc(p);
nextside(p,side);
end;
// -------------------------
function WtoP(p : integer; side : byte) : TPoint;
//point p on side s to point of ellipse
//use a2,b2,dba,dab
begin
case side of
0 : begin
result.x := p;
result.y := -trunc(dba*sqrt(a2-p*p)+0.25);
end;
1 : begin
result.x := -trunc(dab*sqrt(b2-p*p)+0.25);
result.y := p;
end;
2 : begin
result.x := p;
result.y := trunc(dba*sqrt(a2-p*p)+0.25);
end;
3 : begin
result.x := trunc(dab*sqrt(b2-p*p)+0.25);
result.y := p;
end;
end;//case
end;
// ------------------------- main ------
begin
mx := (x1+x2) div 2; //sort x,y
my := (y1+y2) div 2;
a := abs(x2-x1) shr 1;
b := abs(y2-y1) shr 1;
if (a = 0) or (b = 0) or (a > 1000) or (b > 1000) then exit;
//--
//--- calculate (x1,y1)....(x2,y2) of inner rectangle
a2 := a*a;
b2 := b*b;
ab2 := sqrt(a2 + b2);
x2 := trunc(a2/ab2 + 0.5);
x1 := -x2;
y2 := trunc(b2/ab2 + 0.5);
y1 := -y2;
//
if (x1 = 0) and (y1 = 0) then exit;
//
x3 := x3 - mx; x4 := x4 - mx;
y3 := y3 - my; y4 := y4 - my;
if ((x3=0) and (y3=0)) then x3 := x2;
if ((x4=0) and (y4=0)) then x4 := x2;
//
v1 := b*x3;
v2 := a*y3;
s := a*b/sqrt(v1*v1 + v2*v2);
x := trunc(x3*s + 0.5);
y := trunc(y3*s + 0.5);
//
dba := b/a; //for WtoP procedure
dab := a/b;
//
if (abs(x) <= x2) then //startpoint
begin
if (y3<=0) then beginside := 0 else beginside := 2;
sp := x;
end
else begin
if (x3<0) then beginside := 1 else beginside := 3;
sp := trunc(y3*s+0.5);
end;
v1 := b*x4; //endpoint
v2 := a*y4;
s := a*b/sqrt(v1*v1 + v2*v2);
x := trunc(x4*s + 0.5);
y := trunc(y4*s + 0.5);
if abs(x) <= x2 then
begin
if (y4<=0) then endside := 0 else endside := 2;
ep := x;
end
else begin
if (x4<0) then endside := 1 else endside := 3;
ep := trunc(y4*s+0.5);
end;
nextside(sp,beginside);
nextside(ep,endside);
// ------- draw --------------
repeat
pt := WtoP(sp,beginside);
Dot(mx+pt.x,my+pt.y);
nextPoint(sp,beginside);
until (beginside = endside) and (sp = ep);
end;


