The theorem of Ptolemy

Ptolemy lived in Alexandria around the year 0.
We owe him the next theorem of plane geometry:
    In a cyclic quadrilateral the product of the diagonals equals the sum
    of the products of the opposite sides.
In picture:


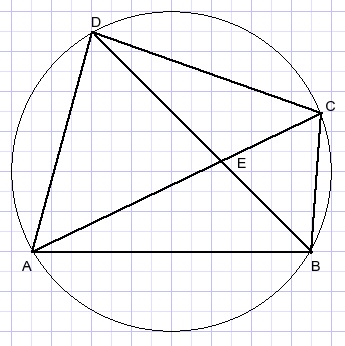
    AC.BD = BC.AD + AB.CD
Thsi article supplies the proof and adds an application.

This proof uses similarity of triangles, the Thales lemma and Stewart's theorem.

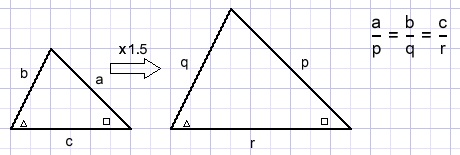
Brief refresher

Similarity
Triangles with equal angles are similar, their sides have equal ratio's:



Thales lemma



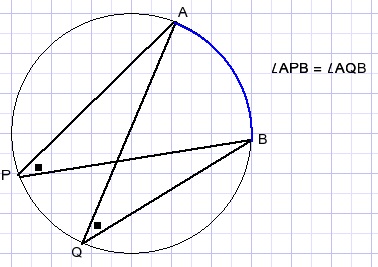
Marked angles are equal bacause they span the same arc of the circle.

Stewart's theorem



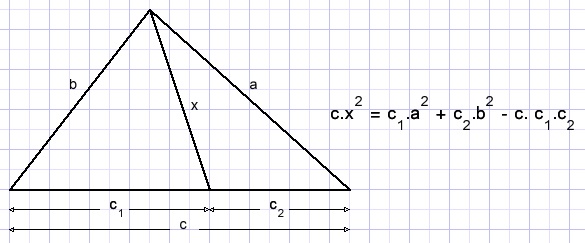
The proof is [HERE]

The theorem of Ptolemy




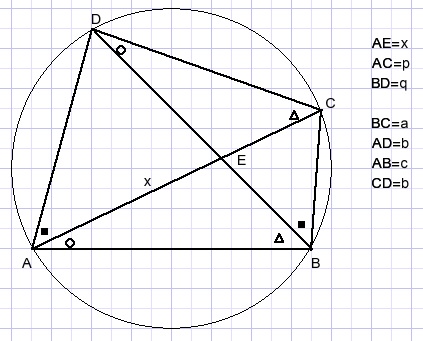
Proof that:
    p.q = a.b + c.d
Equal angles are marked equal (see Thales lemma).
AE=x and we calculate lines BE and DE
and next the theorem of Stewart is applied in ΔABD.


Note: stelling = theorem


Application


Below is pictured a regular heptagon with an intriguing relation:


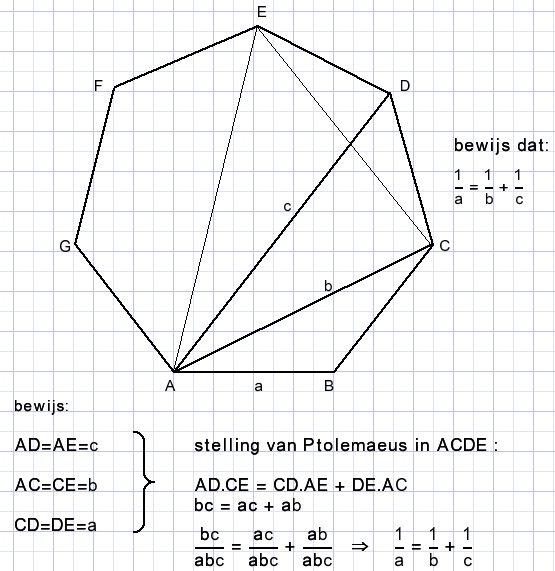
Note: bewijs=proof

A very simple proof, thanks to Ptolemy's theorem.

This problem was found in FaceBook group "Classical Mathematics".
Solution by Kenny Lao.