
 |
Cursus Algebra (5) |
| 1 |
| a p |
| 1 |
| a −p |
 Wortels
Wortels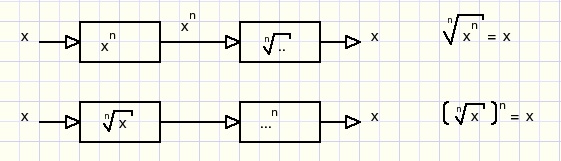
| 2 \ | 3 |
| \ | 3 |
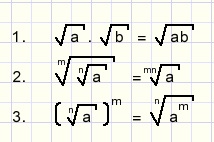
| \ | x 2 + 27 |
 Breuken als exponent
Breuken als exponent
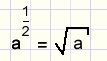
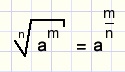
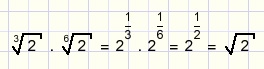
 ExponentiŽle functies
ExponentiŽle functies Stel eens dat een plant zich jaarlijks vermeerdert volgens de formule {M: massa in kg, t: jaren}
Stel eens dat een plant zich jaarlijks vermeerdert volgens de formule {M: massa in kg, t: jaren}
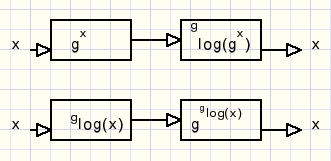

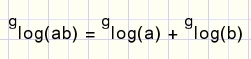
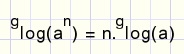
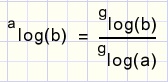
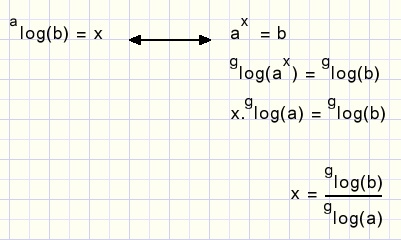
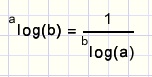
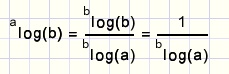
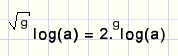
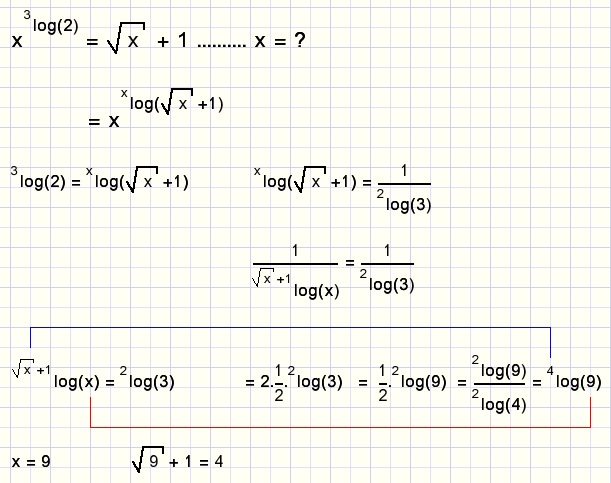
 De groeisnelheid van exponentiŽle functies
De groeisnelheid van exponentiŽle functies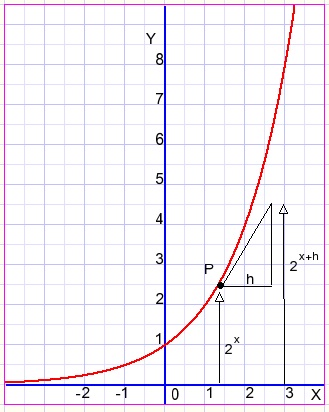
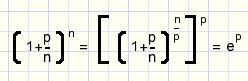
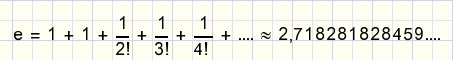
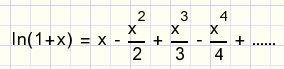
 Test
Test